Dans la suite, 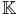 désigne le corps
désigne le corps 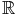 ou le corps
ou le corps 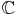 et E est un
et E est un 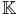 -espace vectoriel.
-espace vectoriel.
Dans la suite, 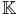 désigne le corps
désigne le corps 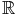 ou le corps
ou le corps 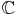 et E est un
et E est un 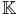 -espace vectoriel.
-espace vectoriel.
Définition :
Une application d : E × E
|
Définition :
Une application
|
Proposition :
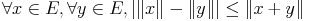 |
Exemples :
Soit {e1; e2; ...; ed} la base canonique de 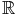 , sur
, sur 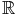
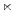 on définit pour tout x
on définit pour tout x 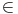
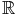
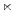 avec
x = x1e1 + x2e2 + ... + xded les normes suivantes :
avec
x = x1e1 + x2e2 + ... + xded les normes suivantes :
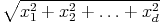 (norme
euclidienne)
(norme
euclidienne)
Cette norme dérive du produit scalaire défini par < x|y >= x1y1 + x2y2 + ... + xdyd
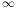 (x) = ||x||
(x) = ||x||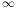 = max{|xi|/1 < i < d}
(norme
uniforme
ou
norme
du
joueur
d’échec
car
elle
correspond
à
la
distance
séparant
deux
cases
pour
un
roi
du
jeu
d’échec)
= max{|xi|/1 < i < d}
(norme
uniforme
ou
norme
du
joueur
d’échec
car
elle
correspond
à
la
distance
séparant
deux
cases
pour
un
roi
du
jeu
d’échec)
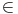 [1; +
[1; +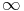 [,Np(x) = ||x||p =
[,Np(x) = ||x||p = 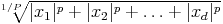 qui
généralise
les
deux
premières
normes
citées.
qui
généralise
les
deux
premières
normes
citées.
L’utilisation
de
l’indice
infini
pour
la
norme
uniforme
vient
du
fait
que
celle-ci
s’obtient
en
prenant
la
limite
de
norme
p
en
+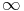 .
.
Définition :
Un espace vectoriel E sur lequel est défini une norme est appelé espace vectoriel normé. On note alors (E; |
Définition :
On appelle distance induite par une norme sur un espace vectoriel normé
(E, |
Définition :
Deux normes |
Théorème :
Dans un espace vectoriel normé de dimension finie, toutes les normes sont équivalentes. |
preuve (peut être omise en première lecture) :
Soit E un espace vectoriel de dimension finie d et |||| une norme sur E. Il suffit de démontrer qu’elle est équivalente à la norme ||||1.
Soit {e1; e2; ...; en} une base de E.
 x
x  E,x =
E,x = 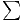 i=1dx
iei on a : ||x|| = ||
i=1dx
iei on a : ||x|| = ||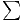 i=1dxiei||<
i=1dxiei||<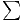 i=1d|x
i|||ei||<
(
i=1d|x
i|||ei||<
(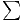 i=1d|x
i|)max{||ei||/i
i=1d|x
i|)max{||ei||/i 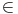 {1; ...; d}}.
{1; ...; d}}.
On pose M = max{||ei||/i 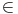 {1; ...; d}}. D’où ||x||< M||x||1.
{1; ...; d}}. D’où ||x||< M||x||1.
D’autre part ||||1 est continue sur sur la sphère unité S1 pour la norme ||||1 donc
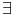 m
m 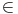
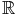 +*/m = inf{||x||
1/x
+*/m = inf{||x||
1/x 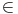 S1}.
S1}.
Pour x 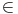 E on a alors
E on a alors 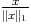
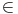 S1 donc ||
S1 donc ||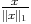 ||> m c’est à dire
||> m c’est à dire 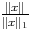 > m et
||x||> m||x||1.
> m et
||x||> m||x||1.
Remarque :
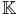 ),
les
normes
||||1
et
||||
),
les
normes
||||1
et
||||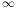 ne
sont
pas
équivalentes.
ne
sont
pas
équivalentes.
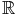 ou
ou
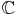 .
.
Par
exemple,
considérons
dans
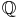 2
considéré
comme
espace
vectoriel
sur
2
considéré
comme
espace
vectoriel
sur
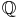 les
deux
normes
N1(r; r') = |r| + |r'|
et
N(r; r') = |r - r'
les
deux
normes
N1(r; r') = |r| + |r'|
et
N(r; r') = |r - r'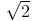 |.
|.
Soit
(an)n
et
(bn)n
deux
suites
d’entiers
naturels
non
nuls
telles
que
la
suite
(an/bn)
converge
vers
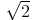 .
.
On
a
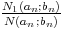 =
= 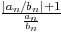 -
-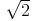 |
qui
tend
vers
+
|
qui
tend
vers
+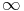 quand
n
tend
vers
l’infini,
ce
qui
montre
qu’il
n’existe
pas
de
constante
k
telle
que
N1 < kN2.
quand
n
tend
vers
l’infini,
ce
qui
montre
qu’il
n’existe
pas
de
constante
k
telle
que
N1 < kN2.
Dans ce qui suit, E est un espace vectoriel normé (E;  ).
).
Définition :
Soient a
|
Définition :
|
Définition :
|
Exemples :
Preuve :
En effet, soit B(a; r) une boule ouverte de centre a et de rayon r. Pour tout point
x de B(a; r), on a  < r. Il existe donc
< r. Il existe donc 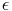 > 0 tel que
> 0 tel que  +
+ 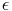 < r(
prendre
< r(
prendre 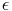 =
= 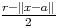 ). Par suite, pour tout y appartenant à B(x;
). Par suite, pour tout y appartenant à B(x; 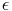 ), on a
), on a
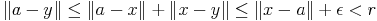
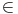 B(a; r) d’où B(x;
B(a; r) d’où B(x; 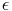 )
) 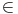 B(a; r). Ceci justifie que pour tout point de
B(a; r), il existe une boule ouverte centrée en ce point et incluse dans B(a; r)
donc B(a; r) est un ouvert.
B(a; r). Ceci justifie que pour tout point de
B(a; r), il existe une boule ouverte centrée en ce point et incluse dans B(a; r)
donc B(a; r) est un ouvert.Proposition :
|
Preuve :
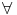 x
x 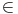
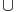 i
i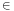 IOi,
IOi, 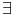 i
i 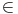 I, x
I, x 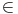 Oi.
Puisque
Oi
est
un
ouvert,
il
existe
une
boule
ouverte
de
centre
x
incluse
dans
Oi
donc
dans
Oi.
Puisque
Oi
est
un
ouvert,
il
existe
une
boule
ouverte
de
centre
x
incluse
dans
Oi
donc
dans
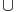 i
i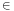 IOi,
ce
qui
justifie
que
pour
tout
point
de
la
réunion
des
Oi
pour
i
IOi,
ce
qui
justifie
que
pour
tout
point
de
la
réunion
des
Oi
pour
i 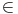 I,
il
existe
une
boule
ouverte
centrée
en
ce
point
et
incluse
dans
cette
réunion.
Par
conséquent
I,
il
existe
une
boule
ouverte
centrée
en
ce
point
et
incluse
dans
cette
réunion.
Par
conséquent
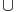 i
i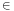 IOi
est
un
ouvert.
IOi
est
un
ouvert.
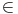 {1; ...; n},
pour
tout
i
{1; ...; n},
pour
tout
i 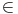 {1; ...; n},
Oi
étant
un
ouvert,
il
existe
une
boule
ouverte
de
centre
x
et
rayon
ri > 0
incluse
dans
Oi.
En
désignant
par
r
le
minimum
des
ri
pour
i
{1; ...; n},
Oi
étant
un
ouvert,
il
existe
une
boule
ouverte
de
centre
x
et
rayon
ri > 0
incluse
dans
Oi.
En
désignant
par
r
le
minimum
des
ri
pour
i 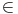 {1; ...; n},
la
boule
ouverte
de
centre
x
et
de
rayon
r
est
donc
incluse
dans
{1; ...; n},
la
boule
ouverte
de
centre
x
et
de
rayon
r
est
donc
incluse
dans
 i
i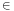 {1;...;n}
qui
est
donc
un
ouvert.
{1;...;n}
qui
est
donc
un
ouvert.
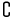
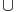 i
i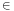 {1;...;n}Fi =
{1;...;n}Fi =  i
i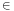 {1;...;n}
{1;...;n}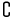 Fi.
Or
les
Fi
étant
fermés,
leurs
complémentaires
sont
fermés
et
d’après
les
propriétés
précédentes
l’intersection
des
complémentaires
est
encore
un
ouvert,
ce
qui
signifie
que
la
réunion
des
Fi
est
fermé.
Fi.
Or
les
Fi
étant
fermés,
leurs
complémentaires
sont
fermés
et
d’après
les
propriétés
précédentes
l’intersection
des
complémentaires
est
encore
un
ouvert,
ce
qui
signifie
que
la
réunion
des
Fi
est
fermé.
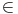 I
est
un
ouvert.
I
est
un
ouvert.
Définition :
Soit a 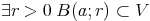 |
Preuve :
Si V est un voisinage de a alors il existe un ouvert O contenant a et inclus dans V . Or O étant ouvert et contenant a, il existe par définition d’un ouvert, une boule ouverte de centre a contenue dans O. En appelant r son rayon on a la première implication.
Réciproquement, s’il existe une boule ouverte de centre a et de rayon r > 0 contenue dans V , comme une boule ouverte est un ouvert, V contient bien un ouvert contenant a.
Propriétés :
Soit a
|
Preuve :
Proposition :
Preuve :
Immédiat.
Définition :
Soient A une partie de E et x
|
Proposition :
Soient A une partie de E et x
|
Définition :
Soit A une partie de E.
|
Définition :
Soient A une partie de E et a un point de A.
|
Proposition :
Proposition :
Définition :
Définition :
Une partie A est dite dense dans E si son adhérence est égale à l’espace E,
c’est à dire si |
Exemple :
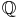 est dense dans
est dense dans 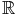 .
.
Remarque :
Les boules, les ouverts, les fermés, les points adhérents ou intérieurs à une partie sont définis à partir d’une norme pour un espace vectoriel normé.
Or, un espace vectoriel normé peut être muni de plusieurs normes.
Il se pose alors la question de savoir si le fait de changer de norme changera la nature des objets ainsi définis.
On a vu que toutes les normes sont équivalentes dans un espace vectoriel normé de dimension finie, cela signifie que la notion d’ouverts, de fermés, de points adhérents, de points intérieurs, mais aussi de limite de suites dépend uniquement de l’espace et pas de la norme choisie.
Cela permet en particulier de choisir la norme la mieux adaptée à la situation étudiée.