Soit (fn)n une suite de fonctions fn définies sur R et à valeurs réelles.
la suite (fn)n tend vers 0 quand n tend vers l'infini est une condition :On considère la suite de fonctions (fn)n avec fn définie sur R+ par :
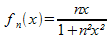
Cette suite de fonctions converge :On considère la suite de fonctions (fn)n avec fn définie sur R+ par :
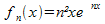
Cette suite de fonctionsLa convergence uniforme d'une série de fonctions définies sur un intervalle I de R et à valeurs réelles implique :
La convergence uniforme d'une série de fonctions définies sur tous les compacts d'un intervalle I de R et à valeurs réelles implique :
On considère une série de fonctions (fn)n avec fn définie sur une partie X de R+ et à valeurs réelles.
On suppose que la série est uniformément convergente sur tout compact de l'intervalle I.
Alors :On considère la suite de fonctions (fn)n avec fn définie sur R+ par :
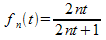
Cette suite de fonctions converge :