|
Dans toute la suite, on se donne une suite (un)n de nombres réels.
Définition :
|
Définition :
|
définition :
Une propriété P(n) est vraie à partir d’un certain rang s’il existe un entier N tel que pour tout entier n > N P(n) est vraie. |
Définition :
|
Proposition :
Si (un)n a une limite l alors elle est unique . On la note lim n |
preuve :
Nous ne traitons que le cas où (un)n possède deux limites finies distinctes l et l'.
Il existe alors  > 0 tel que ]l -
> 0 tel que ]l -  ; l +
; l +  [
[ ]l'-
]l'-  ; l' +
; l' +  [= Ø.
[= Ø.
Comme (un)n tend vers l, 

 /
/ n > N,un
n > N,un  ]l -
]l -  ; l +
; l +  [ ;.
[ ;.
De même,  N
N 
 /
/ n > N',un
n > N',un  ]l'-
]l'-  ; l' +
; l' +  [.
[.
Par conséquent,  n > max(N,N'),un
n > max(N,N'),un  ]l -
]l -  ; l +
; l +  [
[ ]l'-
]l'-  ; l' +
; l' +  [ :
contradiction.
[ :
contradiction.
Proposition :
Toute suite réelle (un)n convergente vers un réel l est bornée. |
Preuve :
Puisque (un)n est convergente vers l, pour  = 1, il existe un entier n tel que
pour tout entier n supérieur ou égal à N on a |un - l| < 1 donc -1 < un - l < 1
ou encore l - 1 < un < l + 1. Par conséquent, on a pour tout entier n,
un < max{u0; u1; ...; uN-1; l + 1} et un > max{u0; u1; u2; ...; uN-1; l - 1}.
= 1, il existe un entier n tel que
pour tout entier n supérieur ou égal à N on a |un - l| < 1 donc -1 < un - l < 1
ou encore l - 1 < un < l + 1. Par conséquent, on a pour tout entier n,
un < max{u0; u1; ...; uN-1; l + 1} et un > max{u0; u1; u2; ...; uN-1; l - 1}.
Proposition :
Soient
|
Preuve :
• Pour tout  strictement positif, (un)n étant convergente,
strictement positif, (un)n étant convergente,
 N1 > 0,
N1 > 0,  n > N1, |un - l| <
n > N1, |un - l| <  . De même, (vn)n étant convergente,
. De même, (vn)n étant convergente,
 N2 > 0,
N2 > 0,  n > N2, |vn - l| <
n > N2, |vn - l| < 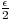 .
.
Par suite,  n > max N1; N2, |un + vn - (l + l')| < |un - l| + |vn - l'| <
n > max N1; N2, |un + vn - (l + l')| < |un - l| + |vn - l'| <  ce
qui montre que la suite (un + vn)n converge vers l + l'.
• Même méthode que précédemment.
• (vn)n étant bornée, il existe M > 0 tel que pour tout entier n, on a vn inférieur
ou égal à M.
ce
qui montre que la suite (un + vn)n converge vers l + l'.
• Même méthode que précédemment.
• (vn)n étant bornée, il existe M > 0 tel que pour tout entier n, on a vn inférieur
ou égal à M.
Comme (un)n converge vers 0, pour tout  strictement positif, il existe un entier
N tel que pour tout entier n supérieur à N on a |un - 0| <
strictement positif, il existe un entier
N tel que pour tout entier n supérieur à N on a |un - 0| <  .
.
D’où |unvn| <  M ce qui montre que (unvn)n est convergente vers 0.
• Soit
M ce qui montre que (unvn)n est convergente vers 0.
• Soit  > 0. (un)n et (vn)n étant convergentes, elles sont respectivement bornées
par deux réels M et M'. On a pour tout entier n,
> 0. (un)n et (vn)n étant convergentes, elles sont respectivement bornées
par deux réels M et M'. On a pour tout entier n,
|unvn - ll'| = |unvn - unl' + l'un - ll'| < |un||(vn - l')| + |l'||un - l| puis
M|vn - l'| + |l'||un-l|. On utilise ensuite la définition de la convergence des
deux suites pour majorer |un - l| par 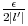 et |vn - l'| par
et |vn - l'| par  .
• l'
.
• l' 0 implique que |l'| > 0.
0 implique que |l'| > 0.
Comme (vn)n converge vers l', pour  =
=  , il existe un entier N tel que pour
tout entier n supérieur ou égal à N on a |vn - l'| <
, il existe un entier N tel que pour
tout entier n supérieur ou égal à N on a |vn - l'| <  . Avec
||vn|-|l'|| < |vn - l'| on obtient donc ||vn|-|l'|| <
. Avec
||vn|-|l'|| < |vn - l'| on obtient donc ||vn|-|l'|| <  c’est à dire
0 < |l'|-
c’est à dire
0 < |l'|- < ||vn| ce qui assure que pour tout n supérieur ou égal à N, la suite
(vn)n est bien définie.
< ||vn| ce qui assure que pour tout n supérieur ou égal à N, la suite
(vn)n est bien définie.
Pour montrer la convergence, on utilise le fait que pour tout n entier supérieur ou
égal à N, | -
- | = |
| = | -
- |. (vn)n est minorée car convergente par un
nombre m supérieur à 0 strictement à partir d’un certain rang. La convergence de
(vn)n permet alors d’assurer que la quantitée ci-dessus peut-être rendue aussi
petite que l’on veut ce qui justifie la convergence de (
|. (vn)n est minorée car convergente par un
nombre m supérieur à 0 strictement à partir d’un certain rang. La convergence de
(vn)n permet alors d’assurer que la quantitée ci-dessus peut-être rendue aussi
petite que l’on veut ce qui justifie la convergence de ( )n vers
)n vers  . On utilise
ensuite le produit de (un)n par (
. On utilise
ensuite le produit de (un)n par ( )n pour obtenir la convergence de (
)n pour obtenir la convergence de ( )n vers
)n vers  .
.
Proposition :
Soient (un)n et (vn)n deux suites réelles avec (un)n qui tend vers +
|
Définition :
On appelle suite extraite (ou sous suite) de (un)n une suite dont le terme
général est u |
Définition :
Soit a  |
Proposition :
Les assertions suivantes sont équivalentes :
|
Preuve :
 > 0
donné,
pour
N = 1,
> 0
donné,
pour
N = 1, n > N/|un - a| <
n > N/|un - a| <  ,i.e.,un
,i.e.,un  ]a -
]a -  ; a +
; a +  [.
On
pose
r1 = n.
[.
On
pose
r1 = n.
Supposons
rk
construit
pour
tout
k < n,
vérifiant
 k < n,uk
k < n,uk  ]a -
]a -  ; a +
; a +  [
et
[
et
 k < n + 1,rk+1 > rk.
k < n + 1,rk+1 > rk.
Alors
pour
N = rn, p > N/|up - a| <
p > N/|up - a| <  .
On
pose
rn+1 = p.
.
On
pose
rn+1 = p.
Par
récurrence,
on
a
donc
construit
une
suite
infinie
de
termes
un
tous
distincts
et
vérifiant
un  ]a -
]a -  ; a +
; a +  [.
[.
 ; a +
; a +  [,
soit
up
tel
que
|up - a| < 1,
on
pose
[,
soit
up
tel
que
|up - a| < 1,
on
pose
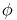 (1) = p.
(1) = p.
Supposons
construite
pour
tout
k < n
une
sous
suite
(u (k))
telle
que
(k))
telle
que
 k < n,|u
k < n,|u (k) - a| < 1/k,
alors
pour
(k) - a| < 1/k,
alors
pour
 = 1/(n + 1),
= 1/(n + 1), r >
r > 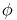 (n)/|ur - a| < 1/(n + 1)
(n)/|ur - a| < 1/(n + 1)
Ainsi
on
construit
par
récurrence
une
sous
suite
extraite
de
(un)
qui
tend
vers
a :
en
effet,
Soit
 > 0,
> 0, k
k 
 */
*/ <
<  et
et
 n > k,|u
n > k,|u (n) - a| <
(n) - a| <  <
< <
<  .
.
 (n))n
qui
tend
vers
a,
alors
pour
tout
(n))n
qui
tend
vers
a,
alors
pour
tout
 strictement
positif
et
pour
tout
N
strictement
positif
et
pour
tout
N 
 ,
il
existe
p
,
il
existe
p 
 tel
que
tel
que
 n > p,|u
n > p,|u (n) - a| <
(n) - a| <  donc,
donc,
 n > max(N,p),|u
n > max(N,p),|u (n) - a| <
(n) - a| < 
Remarque :
Un point a est adhérent à une partie A de  ssi tout intervalle de la forme
]a -
ssi tout intervalle de la forme
]a -  ; a +
; a +  [ avec
[ avec  > 0 contient un point de A.
> 0 contient un point de A.
Il ne faut pas confondre ici valeur d’adhérence de la suite (un)n et point adhérent
à l’ensemble {un/n 
 } : toute valeur d’adhérence de la suite est point adhérent
à {un/n
} : toute valeur d’adhérence de la suite est point adhérent
à {un/n 
 }. mais la réciproque est fausse : ainsi toute valeur up de la suite est
adhérent à {un/n
}. mais la réciproque est fausse : ainsi toute valeur up de la suite est
adhérent à {un/n 
 } mais n’est pas en général valeur d’adhérence de (un)n.
} mais n’est pas en général valeur d’adhérence de (un)n.
Proposition :
(un)n tend vers une limite l ssi toute suite extraite tend vers l. |
Preuve :
Si toute suite extraite tend vers l, en particulier (un)n tend vers l.
Réciproquement, si (un)n tend vers une limite l que l’on supposera finie, les
autres cas se démontrant de la même manière, on se donne une suite extraite
(u (n))n de la suite (un)n.
(n))n de la suite (un)n.
Alors 
 > 0,
> 0, p
p 
 ,
, n > p,|un - l| <
n > p,|un - l| <  donc,
donc, 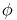 étant strictement croissante
de
étant strictement croissante
de  dans
dans  on a
on a 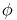 (n) > n pour tout n
(n) > n pour tout n 
 et donc |u
et donc |u (n) - l| <
(n) - l| <  pour tout
n > p.
pour tout
n > p.
Exemple :
(un)n définie par un = sin( ) n’est pas convergente.
) n’est pas convergente.
Preuve :
En effet, u14n = sin( ) = sin(2n
) = sin(2n ) = 0 pour tout n
) = 0 pour tout n 
 donc (u2n)n
converge vers 0 alors que
u14n+1 = sin(
donc (u2n)n
converge vers 0 alors que
u14n+1 = sin( ) = sin(2n
) = sin(2n +
+  ) = sin(
) = sin( )(-1)2n = sin(
)(-1)2n = sin( ) pour tout
n
) pour tout
n 
 et (u14n+1)n converge donc vers sin(
et (u14n+1)n converge donc vers sin( ).
).
Exemple :
(un)n converge vers l ssi les suites extraites (u2n)n et (u2n+1)n convergent vers l.
Preuve :
La condition nécessaire est évidente d’après la proposition III. Supposons donc que (u2n)n et (u2n+1)n tendent toutes les deux vers la même limite l.

 > 0,
> 0, N1
N1 
 /
/ n > N1,|u2n-1 - l| <
n > N1,|u2n-1 - l| <  et
et
 N2
N2 
 /
/ n > N2|u2n+1 - l| <
n > N2|u2n+1 - l| < 
On pose N = max{2N1; 2N2 + 1}. Pour tout n > N, si n est pair alors n = 2k
et k > N1 donc |u2k - l| = |un - l| <  sinon n est impair, n = 2k + 1, k > N2
donc |u2k+1 - l| = |un - l| <
sinon n est impair, n = 2k + 1, k > N2
donc |u2k+1 - l| = |un - l| < 
Proposition :
Soient (un)n une suite réelle convergente, l
|
Théorème "de la limite monotone" :
Si (un)n est croissante (resp. décroissante) alors : limn = supn{un} (resp. infn{un}) et (un)n est convergente ssi elle est majorée (resp. minorée). |
Preuve :
Par définition de la borne supérieure,

 > 0,
> 0, N
N 
 ,supn{un}-
,supn{un}-  < uN < supn{un} donc, (un)n étant croissante,
< uN < supn{un} donc, (un)n étant croissante,
 n > N,supn{un}-
n > N,supn{un}-  < uN < un < supn{un}. Même type de preuve pour le
cas décroissant.
< uN < un < supn{un}. Même type de preuve pour le
cas décroissant.
Théorème "des gendarmes" :
Soient (xn)n, (un)n et (yn)n trois suites réelles. |
preuve :
 > 0.
limnxn = l
donne
l’existence
de
N'
> 0.
limnxn = l
donne
l’existence
de
N'
 ',
', n > N',xn > l -
n > N',xn > l -  limnyn = l
donne
l’existence
de
N''
limnyn = l
donne
l’existence
de
N''
 ,
, n > N'',yn < l +
n > N'',yn < l +  Pour
tout
n > max{N; N'; N''}
on
a
donc
l -
Pour
tout
n > max{N; N'; N''}
on
a
donc
l -  < xn < un < yn < l +
< xn < un < yn < l +  .
.

 ,
comme
limnxn = +
,
comme
limnxn = + ,
,
 N'
N'
 ,
, n > N',xn > M
donc
pour
tout
n > max{N; N'}
on
a
un > xn > M.
n > N',xn > M
donc
pour
tout
n > max{N; N'}
on
a
un > xn > M.

 ,
comme
limnyn = -
,
comme
limnyn = - ,
,
 N''
N''
 ,
, n > N'',yn < M
donc
pour
tout
n > max{N; N''}
on
a
un < yn < M.
n > N'',yn < M
donc
pour
tout
n > max{N; N''}
on
a
un < yn < M.Proposition :
Soient (un)n et (vn)n deux suites réelles. Si à partir d’un certain rang un < vn
et si (un)n tend vers + |
Définition :
Deux suites réelles (un)n et (vn)n sont dites adjacentes si les deux suites sont monotones, l’une croissante, l’autre décroissante et si (un - vn)n converge vers 0. |
Proposition :
Deux suites adjacentes sont convergentes vers une limite commune. |
Théorème des segments emboîtés :
Soit (In)n une suite de segments In = [an; bn] tels que
Alors il existe un réel l |
Preuve :
Du fait que pour tout entier n, In+1  In on déduit que an+1 > an et bn+1 < bn.
La suite (an)n est donc croissante, la suite (bn)n décroissante. En outre,
(bn - an)n converge vers à donc les suites (an)n et (bn)n sont adjacentes et sont
donc convergentes vers une limite commune l.
In on déduit que an+1 > an et bn+1 < bn.
La suite (an)n est donc croissante, la suite (bn)n décroissante. En outre,
(bn - an)n converge vers à donc les suites (an)n et (bn)n sont adjacentes et sont
donc convergentes vers une limite commune l.
S’il existe N 
 tel que l
tel que l IN, alors l > bN ou l < aN. On peut supposer que
l < an, le raisonnement serait identique dans l’autre cas. Il existe donc
IN, alors l > bN ou l < aN. On peut supposer que
l < an, le raisonnement serait identique dans l’autre cas. Il existe donc  > 0 tel
que pour tout n < N, l +
> 0 tel
que pour tout n < N, l +  < aN < an c’est à dire l - an >
< aN < an c’est à dire l - an >  ce qui impose que
(an)n ne converge pas vers l en contradiction avec ce qui a été justifié
précédemment. Par conséquent
ce qui impose que
(an)n ne converge pas vers l en contradiction avec ce qui a été justifié
précédemment. Par conséquent  n
n 
 , l
, l 
 In.
In.
Soit l' l, alors il existe
l, alors il existe  > 0 tel que |l - l'| >
> 0 tel que |l - l'| >  . Or (bn - an)n étant
convergente vers 0, il existe N tel que |bN - aN| <
. Or (bn - an)n étant
convergente vers 0, il existe N tel que |bN - aN| <  . Si l'
. Si l' IN alors
|l - l'| < |l - aN| + |l'- aN| <
IN alors
|l - l'| < |l - aN| + |l'- aN| <  +
+  <
<  , contrairement à ce qui précède. Donc
l'
, contrairement à ce qui précède. Donc
l' In et
In et  In = {l}.
In = {l}.
Théorème "de Bolzano-Weierstrass" :
De toute suite bornée de nombres réels, on peut extraire une sous suite convergente. |
preuve :
Soit (un)n une suite bornée. Il existe M 
 tel que -M < un < M.
tel que -M < un < M.
Construisons une suite (In)n d’intervalles de la forme [an; bn] vérifiant In
contient une infinité de termes de la suite (un)n, le diamètre  (In) <
(In) < (b0 - a0)
où
(b0 - a0)
où  (In) désigne le diamètre de In et In+1
(In) désigne le diamètre de In et In+1  In.
In.
On pose a0 = -M, b0 = M et donc I0 = [-M; M] qui vérifie de manière évidente les trois conditions précédentes.
Supposons Ik = [ak; bk] construit jusqu’à un rang n.
Alors [an;  ] ou [
] ou [ ; bn] contient une infinité de termes de la suite (un)n.
; bn] contient une infinité de termes de la suite (un)n.
Si [an;  ] contient une infinité de termes de la suite, on pose an+1 = an et
bn+1 =
] contient une infinité de termes de la suite, on pose an+1 = an et
bn+1 =  sinon on pose an+1 =
sinon on pose an+1 =  et bn+1 = bn.
et bn+1 = bn.
Dans les deux cas, In+1  In et
bn+1 - an+1 =
In et
bn+1 - an+1 =  <
<
 (b0 - a0) <
(b0 - a0) < (b0 - a0) donc In+1 vérifie les trois
conditions énoncées.
(b0 - a0) donc In+1 vérifie les trois
conditions énoncées.
Par récurrence on construit donc la suite (In)n.
Construisons ensuite une sous suite (u (n))n de la suite (un)n telle que
(n))n de la suite (un)n telle que
 n
n 
 u
u (n)
(n)  In.
In.
On pose 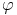 (0) = 0 et de manière évidente u0
(0) = 0 et de manière évidente u0  I0 = [a0; b0]
I0 = [a0; b0]
Supposons construite jusqu’à un rang n, 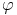 (k)/0 < k < n vérifiant
(k)/0 < k < n vérifiant
 k < n - 1,
k < n - 1,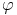 (k + 1) >
(k + 1) > 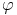 (k) et
(k) et  k
k  {0; ...; n}
{0; ...; n}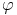 (k)
(k)  Ik.
Ik.
On a In+1  In et In+1 possède une infinité de termes de la suite (un)n. Il existe
donc p >
In et In+1 possède une infinité de termes de la suite (un)n. Il existe
donc p > 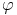 (p)/up
(p)/up  In+1. On pose alors
In+1. On pose alors  (n + 1) = p. et qui vérifie les
conditions voulues. Par récurrence, on construite donc la suite (u
(n + 1) = p. et qui vérifie les
conditions voulues. Par récurrence, on construite donc la suite (u (n))n.
(n))n.
Par construction, cette sous suite converge vers  In qui est un singleton {l} avec
l
In qui est un singleton {l} avec
l 
 d’après le théorème des segments emboîtés.
d’après le théorème des segments emboîtés.