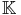 =
= 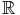 ou
ou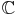 .
.
Dans ce qui suit, on considère un corps 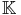 =
= 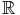 ou
ou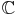 .
.
Définition :
Une suite arithmétique est donnée par son premier terme u0 et sa raison r : 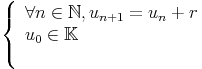 |
Proposition :
|
Preuve :
Par récurrence, les deux propriétés sont trivialement vraies au rang n = 0. Si
elles sont vraies au rang n 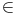
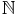 , on a :
un+1 = un + r = u0 + nr + r = u0 + (n + 1)r et
u1+...+un+1 = (n+1)u0+r
, on a :
un+1 = un + r = u0 + nr + r = u0 + (n + 1)r et
u1+...+un+1 = (n+1)u0+r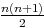 +un+1 = (n+1)u0+r
+un+1 = (n+1)u0+r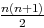 +u0+(n+1)r =
(n + 2)u0 + r
+u0+(n+1)r =
(n + 2)u0 + r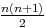 + r
+ r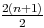 = (n + 2)u0 +
= (n + 2)u0 + 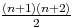 Donc les propriétés sont
vraies au rang n + 1 et par récurrence, elles sont donc vraies pour tout n
Donc les propriétés sont
vraies au rang n + 1 et par récurrence, elles sont donc vraies pour tout n 
 .
.
Définition :
Une suite géométrique est donnée par son premier terme u0 et sa raison q (non nulle en général) : 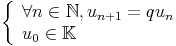 |
Proposition :
|
Preuve :
Par récurrence. Les deux propriétés sont vraies au rang n = 0. Supposons
qu’elles sont vraies à un rang n 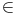
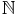 . On a alors un+1 = qun = qqnu
0 = qn+1u
0
d’une part. D’autre part, si q = 1, on a
u1 + ... + un+1 = (n + 1)u0 + un+1 = (n + 1)u0 + u0 = (n + 2)u0 et si q
. On a alors un+1 = qun = qqnu
0 = qn+1u
0
d’une part. D’autre part, si q = 1, on a
u1 + ... + un+1 = (n + 1)u0 + un+1 = (n + 1)u0 + u0 = (n + 2)u0 et si q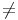 1, on
a u1 + ... + un+1 = u0
1, on
a u1 + ... + un+1 = u0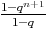 + un+1 = u0
+ un+1 = u0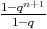 + qn+1u
0 =
u0(
+ qn+1u
0 =
u0(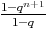 +
+ 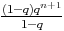 ) = u0
) = u0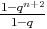 . Les deux propriétés sont donc vraies au rang
n + 2 et par récurrence elles sont vraies pour tout n
. Les deux propriétés sont donc vraies au rang
n + 2 et par récurrence elles sont vraies pour tout n 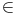
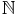 .
.
Définition :
Une suite arithmético-géométrique est définie par : 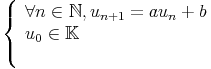 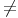 0 et a 0 et a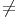 1, sinon on retrouve les suites précédentes. 1, sinon on retrouve les suites précédentes. |
Définition
Une suite particulière est obtenue pour la suite constante l telle que l = al + b.
Cette valeur l est d’ailleurs la limite éventuelle de la suite si elle converge. Soit
(vn)n la suite auxiliaire définie par : 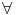 n
n 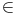
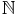 ,vn = un - l
,vn = un - l
On a alors : 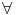 n
n 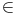
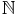 ,vn+1 = avn. Autrement dit, la suite (vn)n est une suite
géométriques de raison a. On a vn = anv
0 et un = l + an(u
0 - l).
,vn+1 = avn. Autrement dit, la suite (vn)n est une suite
géométriques de raison a. On a vn = anv
0 et un = l + an(u
0 - l).
La suite converge donc ssi |a| < 1 ou u0 = l.
Définition :
Une suite récurrente linéaire est définie par : 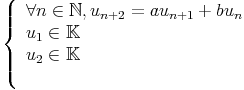 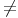 0 0 |
Les suites géométriques rn non nulles solution de cette récurrence vérifient : r2 = ar + b. Soit r solution (éventuellement complexe). Cherchons les autres solutions sous la forme : un = vnrn. On obtient :
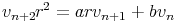
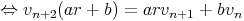
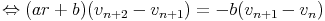
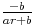 ou
ou 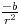 ou enfin r'/r
si r’ est l’autre racine. On a donc : vn - vn-1 = C(
ou enfin r'/r
si r’ est l’autre racine. On a donc : vn - vn-1 = C(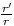 )n, où C est une constante. On en
déduit que : vn = C(
)n, où C est une constante. On en
déduit que : vn = C(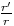 )n + C(
)n + C(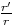 )n-1 + ... + C(
)n-1 + ... + C(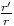 ) + v0.
) + v0.
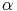 n +
n + 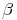 et
un
est
combinaison
des
suites
rn
et
nrn.
et
un
est
combinaison
des
suites
rn
et
nrn.
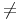 r'
alors
vn
est
de
la
forme
r'
alors
vn
est
de
la
forme
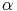 (
(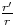 )n +
)n + 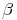 ,
et
un
est
combinaison
de
rn
et
de
r'n.
,
et
un
est
combinaison
de
rn
et
de
r'n.proposition :
Soit la relation de récurrence un+2 = aun+1 + bun. On associe à cette relation l’équation caractéristique r2 = ar + b. L’ensemble des suites solutions forme un espace vectoriel de dimension 2 dont une base est :
|
preuve :
Posons S = {(un)n/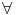 n
n 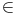
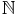 ,un+2 = aun+1 + bun}S est un sous-espace
vectoriel de l’espace vectoriel des suites. Cet espace est de dimension 2. En effet,
considérons les deux suites particulières U et V éléments de S, définies par
U0 = 1 et U1 = 0,V 0 = 0 et V 1 = 1. On prouve facilement par récurrence que
toute suite u de S s’écrit : u = u0U + u1V Cette décomposition est unique. Ceci
prouve que (U; V ) constitue une base de S. Cette base est malheureusement de
peu d’utilité car elle ne permet pas de calculer le terme général de la suite.
Cherchons donc une autre base. Cherchons les éléments de S qui sont des suites
géométriques (rn)n. r doit alors vérifier :
,un+2 = aun+1 + bun}S est un sous-espace
vectoriel de l’espace vectoriel des suites. Cet espace est de dimension 2. En effet,
considérons les deux suites particulières U et V éléments de S, définies par
U0 = 1 et U1 = 0,V 0 = 0 et V 1 = 1. On prouve facilement par récurrence que
toute suite u de S s’écrit : u = u0U + u1V Cette décomposition est unique. Ceci
prouve que (U; V ) constitue une base de S. Cette base est malheureusement de
peu d’utilité car elle ne permet pas de calculer le terme général de la suite.
Cherchons donc une autre base. Cherchons les éléments de S qui sont des suites
géométriques (rn)n. r doit alors vérifier :
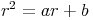
Plusieurs cas sont à considérer :
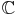 :
:
si le discriminant est non nul, il y a deux suites différentes de raisons r1 et r2. Il n’est pas difficile de montrer que ces deux suites forment un système libre et donc une base de S. Cette base permet de calculer le terme général de toute suite de S ;
si
le
discriminant
est
nul,
alors
il
y
a
une
racine
unique
r,
égale
à
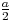 ,
et
b = -
,
et
b = -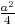 .
Cherchons
une
autre
suite
sous
la
forme
vnrn.
On
obtient
alors :
.
Cherchons
une
autre
suite
sous
la
forme
vnrn.
On
obtient
alors :
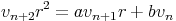
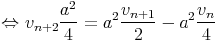
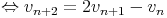
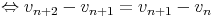
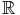 :
:
si le discriminant est positif, c.f. ci-dessus ;
si le discriminant est nul, c.F. ci-dessus ;
si le discriminant est négatif, alors, en tant que sous espace vectoriel complexe, on peut prendre comme base les suites géomériques de raison r1 et r2, nécessairement conjuguées si a et b sont réels. Mais on peut prendre également Re(r1n) et Im(r2n) qui, étant combinaisons linéaires de r1n et r2n sont bien éléments de S, sont réelles, et engendrent S.
Exemples :
Définition :
Une suite est dite récurrente si elle est définie par : un+1 = f(un) pour tout
n |
Dans la suite, on se donne une suite (un)n définie par :
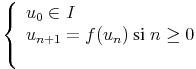
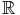 et à valeurs dans I.
et à valeurs dans I.
Proposition :
Si f est croissante sur I alors (un)n est monotone :
|
Preuve :
Montrons par récurrence que pour tout n 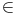
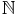 , u(n + 1) - un est du signe de
u1 - u0.
, u(n + 1) - un est du signe de
u1 - u0.
C’est vrai pour n = 0 de manière évidente, supposons la propriété vraie pour un
rang n. On a alors :
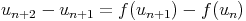
Proposition :
Si f est décroissante, alors les deux suites extraites (u2n)n et (u2n+1)n sont monotones de sens opposé. |
preuve :
Si f est décroissante, f o f est croissante donc par la proposition précédente (u2n)n et (u2n+1)n sont monotones. On a en outre u2n+2 - u2n qui est du même signe que u2 - u0 et u2n+1 - u2n-1 de même signe que u3 - u1. Si f o f(u0) > u0 alors u2 - u0 > 0 et f o f(f(u0)) < f(u0) donc u3 - u1 < 0 donc (u2n+1)n est croissante et (u2n)n est décroissante. Si f o f(u0) < u0, (u2n)n est décroissante et u2n+1)n est croissante.
On suppose dans la suite que f est continue d’un intervalle I fermé dans lui-même.
Proposition :
Si (un)n converge vers l, alors l |
Preuve :
Par continuité de f, si (un)n converge vers l, alors (f(un)n) converge vers f(l), Mais f(un) = un+1 donc par unicité de la limite l = f(l).
Conséquence :
Si f n’a pas de point fixe, (un)n diverge.
Remarques :
 -x
sur
[0; 1]
admet
0
pour
unique
point
fixe
et
la
suite
(un)n
associée
diverge.
-x
sur
[0; 1]
admet
0
pour
unique
point
fixe
et
la
suite
(un)n
associée
diverge.
Preuve :
Soit g : I 
 définie par
définie par  x
x 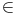 I g(x) = f(x) - x. On a g(a) = f(a) - a > 0,
g(b) = f(b) - b < 0 et g est continue sur I donc par la théorème des valeurs
intermédiaires, il existe c
I g(x) = f(x) - x. On a g(a) = f(a) - a > 0,
g(b) = f(b) - b < 0 et g est continue sur I donc par la théorème des valeurs
intermédiaires, il existe c 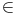 [a; b] tel que g(c) = 0 c’est à dire f(c) = c
[a; b] tel que g(c) = 0 c’est à dire f(c) = c
Dans la suite, on supposera I fermé borné, i.e. I = [a; b] avec a < b.
Proposition :
On suppose f croissante sur I : |
|
Preuve :
On a vu que f admet au moins un point fixe, que (un)n est monotone. Comme elle est bornée, elle admet donc une limite qui ne peut-être qu’un point fixe de f.
Remarque :
Si f est strictement décroissante, f admet un unique point fixe, envisager la convergence de la suite (un)n.
Preuve :
On a vu que f admet un point fixe. Montrons qu’il est unique. Si l1 et l2 sont
deux points fixes distincts, on peut supposer l1 < l2 et on a alors f(l1) > f(l2)
puisque f est strictement décroissante. Or pour i 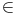 {1; 2}, f(li) = li donc
l1 > l2 ce qui est absurde et montre l’unicité.
{1; 2}, f(li) = li donc
l1 > l2 ce qui est absurde et montre l’unicité.
Proposition :
On suppose f k-contractante sur I, c’est à dire |
preuve :
Sous réserve d’existence, montrons d’abord l’unicité. Si l1 et l2 sont deux points fixes pour f on a donc f(l1) = l1 et f(l2) = l2. Par suite ||l1 - l2|| = ||f(l1) - f(l2)||< k||l1 - l2|| donc (1 - k)||l1 - l2||< 0 ce qui impose l1 - l2|| = 0 d’où l’unicité. Pour l’existence, soit (un)n la suite définie précédemment. Montrons qu’elle est de Cauchy. Soient donc n et p entiers :
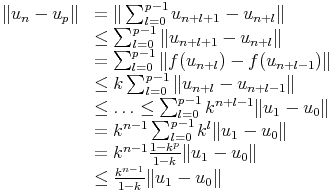
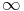 indépendamment de p.
Donc la suite (un)n est de Cauchy dans I complet et par conséquent elle
converge vers une limite l. On a :
indépendamment de p.
Donc la suite (un)n est de Cauchy dans I complet et par conséquent elle
converge vers une limite l. On a :
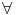 n
n 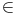
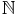 ||l - f(l)|| = ||l - un+1 + f(un) - f(l)||<||l - un+1|| + ||f(un)f(l)||<
||l - un+1|| + k||un - f(l)||. Comme (un)n converge vers l, cette quantité peut
donc être rendue aussi petite que l’on veut et par conséquent l = f(l).
||l - f(l)|| = ||l - un+1 + f(un) - f(l)||<||l - un+1|| + ||f(un)f(l)||<
||l - un+1|| + k||un - f(l)||. Comme (un)n converge vers l, cette quantité peut
donc être rendue aussi petite que l’on veut et par conséquent l = f(l).