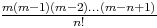On dit que la série |
Dans ce qui suit on considère un espace de Banach E.
Définition :
On dit que la série |
Remarque :
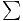 n>0||un|| est une série à termes positifs.
n>0||un|| est une série à termes positifs.
Théorème :
Toute série normalement convergente est convergente. |
Preuve :
Soit 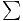 n>0un telle
n>0un telle 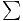 n>0||un|| converge. Soit SN =
n>0||un|| converge. Soit SN = 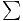 k=0Nu
k et
sN =
k=0Nu
k et
sN = 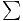 k=0N||u
k||.
k=0N||u
k||.
On a sn+p - sn = 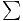 k=1p||u
n+k|| et Sn+p - Sn =
k=1p||u
n+k|| et Sn+p - Sn = 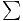 k=1pu
n+k. Donc
k=1pu
n+k. Donc
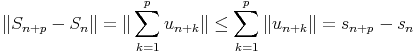
Théorème :
|
Preuve :
Proposition :
Soient (xn)n et (yn)n deux suites positives.
|
Théorème (Séries de Riemann) :
Pour tout |
Application :
Soit 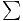 n=0+
n=0+ u
n une série à termes positifs. S’il existe
u
n une série à termes positifs. S’il existe 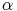
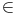 ]1; +
]1; +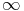 [ tel que
limn
[ tel que
limn
 n
n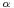 u
n = 0, alors
u
n = 0, alors 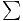 n=0+
n=0+ u
n converge.
u
n converge.
Théorème (Série géométrique) :
Soit r 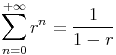 |
Proposition (règle de d’Alembert) :
On suppose que pour tout entier naturel n, un > 0, que (an)n ne s’annule qu’en un
nombre fini de rangs et que lim sup
|
Preuve :
 N ,
N , 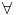 n > N
n > N 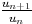 < r
< r
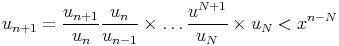
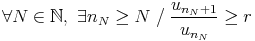
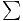 n>0un
diverge.
n>0un
diverge.Proposition (Règle de Cauchy) :
On suppose que pour tout entier naturel n, un > 0 et que lim sup |
Preuve :
 N /
N / 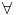 n > N
n > N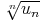 < r
donc
un < rn.
D’après
le
critère
de
comparaison
< r
donc
un < rn.
D’après
le
critère
de
comparaison
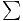 nxn
converge.
nxn
converge.
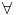 N
N  nN > N /
nN > N / 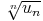 > r
d’où
unN > rnN.
Comme
r > 1,
la
série
diverge.
> r
d’où
unN > rnN.
Comme
r > 1,
la
série
diverge.Remarque :
Le principe de la démonstration des règles de d’Alembert et de Cauchy consiste
à comparer la série à une série géométrique : ces règles ne peuvent donc
s’appliquer que pour une série convergente dont le terme général tend vers zéro
plus vite su’une suite géométrique de raison q 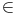 [0; 1[, ou pour une série
divergente dont le terme général tend vers +
[0; 1[, ou pour une série
divergente dont le terme général tend vers +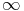 plus vite q’une suite géométrique
de raison q > 1. Cela explique qu’elles ne s’appliquent pas par exemple aux
séries de Riemann puisque qn = o(
plus vite q’une suite géométrique
de raison q > 1. Cela explique qu’elles ne s’appliquent pas par exemple aux
séries de Riemann puisque qn = o(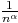 ) pour
) pour 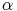 réel et q
réel et q 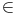 [0; 1[ et
[0; 1[ et 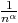 = o(qn)
pour q > 1.
= o(qn)
pour q > 1.
Théorème :
Soit f une fonction de [n0; + |
Soit (un)n la suite définie par 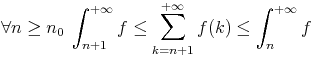 |
Preuve :
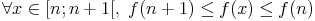
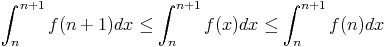
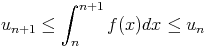
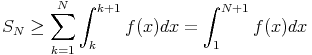
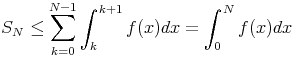
 , si la série converge,
, si la série converge,  1+
1+ f(x)dx converge et si
f(x)dx converge et si
 0+
0+ f(x)dx converge alors la série converge.
f(x)dx converge alors la série converge.Exercice :
Soit (xn)n une suite à temes strictement positifs telle que lim 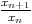 = l. Alors
lim
= l. Alors
lim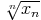 = l. Ainsi si la règle de d’Alembert a échouée, il est inutile d’essayer
celle de Cauchy). Etudier la réciproque.
= l. Ainsi si la règle de d’Alembert a échouée, il est inutile d’essayer
celle de Cauchy). Etudier la réciproque.
Si les règles de d’Alembert et Cauchy ont échouées, on peut essayer la suivante :
Proposition (Règle de Rabbe-Duhamel) :
Soit (xn)n une suite à termes strictement positifs telle que : 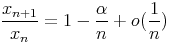
|
Exercice (Séries de Bertrand) :
Pour tout (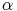 ,
, )
) 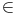
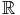 2 fixé,
2 fixé, 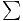 n<2
n<2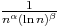 converge ssi :
converge ssi :
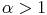
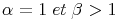
Exercice :
Etudier la nature de la série de terme général un = (-1)n