Séries entières. Rayon de convergence. Propriétés de la somme.

On appelle série entière toute série sum _n>0f_n de fonctions définies de dans par f_n(z) = a_nzⁿ où (a_n)_n est une suite de .

Soit (a_n)_n une suite de . L’ensemble des réels r positifs ou nuls pour lesquels la suite (a_nrⁿ)_n est bornée est non vide car il contient 0.

Sa borne supérieure R, éventuellement infinie, est appelée rayon de convergence de la série entière sum _n>0a_nzⁿ.

Exemple :

Le rayon de convergence de _n>0n!zⁿ est R = 0
Celui de _n>0zⁿ est R = 1.
_n>0 a pour rayon de convergence R = +.

Soit sum _n>0a_nzⁿ une série entière, et soit R son rayon de convergence.

Si |z₀| < R, alors la série entière _n>0a_nz₀ⁿ est absolument convergente donc convergente.
Si |z₀| > R, alors la suite (a_nz₀ⁿ)_n n’est pas bornée donc ne converge pas vers 0 et _n>0a_nz₀ⁿ diverge.
Si 0 < R' < R, notons D(0;R') le disque fermé dans de centre O et de rayon R'. Alors _n>0a_nzⁿ converge uniformément dans .

Preuve :

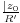On a |a_nz₀ⁿ|<|a_n|()ⁿR'ⁿ pour |z₀| < R' < R. De ce fait, (|a_nR'ⁿ|)_n est bornée. Soit M = sup_n{|a_n|R'ⁿ}. Alors, |a_nz₀ⁿ|< M()ⁿ. Comme < 1, la série _n()ⁿ converge et par comparaison, _na_nz₀ⁿ aussi.
clair
Soit R'' tel que R' < R'' < R et (|a_n|R''ⁿ)_n bornée. Soit M = sup_n{|a_nR''ⁿ}. Alors n 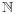|a_nzⁿ|<|a_n|R'ⁿ <|a_n|R''ⁿ()ⁿ < M()ⁿ.

En supposant R0, {z / |z| < R} est appelé disque ouvert de convergence de sum _n>0a_nzⁿ.

Remarque :

Il se peut qu’une série entière sum _n>0a_nzⁿ ne soit pas normalement convergente sur son disque ouvert de convergence. C’est le cas par exemple pour la série entière sum _n>0zⁿ.

Le rayon de convergence R est donné par :

1-= lim sup n V~ |an| R

Règle de D’Alembert :

Soit sum _n>0a_nzⁿ une série entière et soit R son rayon de convergence. On suppose que les coefficients a_n sont non nuls à partir d’un certain rang. Si lim_n| ana+1-
n | = ⁺ {+}, alors R = 1
c (avec R = + si = 0 et R = 0 si = +).

2 Propriétés de la somme

La somme S : z '--> S(z) = sum _n>0a_nzⁿ est continue sur le disque ouvert de convergence.

Preuve :

Soit z₀ D(O;R) et R' > 0 tel que |z₀| < R' < R. Alors sum _na_nzⁿ converge normalement sur D(O;R') donc, z '--> sum _k=0ⁿa_kz^k étant continue pour tout entier n sur D(O;R'), sa somme l’est aussi d’où S est continue sur D(O;R') et donc en particulier en z₀.

Soient sum _n>0a_nzⁿ et sum _n>0b_nzⁿ deux séries entières de rayons R > 0 et R' > 0. On suppose que les sommes de ces deux séries coïncident sur un voisinage de 0. Alors ces deux séries sont identiques : n a_n = b_n.

Preuve :

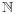Sinon N / a_Nb_N. Soit alors N le plus petit tel. Il existe r > 0 tel que r < R, r < R' et les deux sommes coîncident sur D(O;R). On a alors :

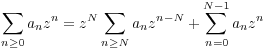
sum sum N sum -1 anzn = zN anzn- N + anzn n>0 n>N n=0

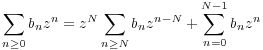
sum n N sum n- N N sum -1 n bnz = z bnz + bnz n>0 n>N n=0

Comme les deux séries sont égales et

n < N - 1 a_n = b_n alors pour tout z

D(O;r), on a sum

_n>Na_nz^n-N = sum

_n>Nb_nz^n-N. En particulier, pour z = 0 on obtient a_N = b_N d’où une contradiction.

La somme S(z) de la série entière sum _n>0a_nzⁿ est une fonction paire (resp. impaire) ssi les a_n de rang impair (resp. pair) sont nuls.

Preuve :

Si sum _na_nzⁿ est paire, sum _na_nzⁿ = sum _na_n(-z)ⁿ pour tout n donc n 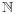a_n = (-1)ⁿa_n et en particulier k 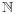a_2k+1 = (-1)a_2k+1 ce qui implique a_2k+1 = 0.

Soit sum _n>0a_ntⁿ une série entière réelle, de rayon de convergence R > 0 et de somme S(t).

S est indéfiniment dérivable sur ] - R;R[ et : $A t (- ]- R; R[, S(k)(t) = sum n(n - 1)...(n - k+ 1)antn- k n>k$
Si [a;b] ] - R;R[ alors : $integral integral b sum b n+1 a S(t)dt = an a t dt n>0$

Lemme :

Pour toute série entière A(z) = sum _n>0a_nzⁿ de rayon de convergence R, les séries entières suivantes ont aussi pour rayon de convergence R :

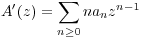
' sum n-1 A (z) = nanz n>0

(k) sum n-k A k (- N A (z) = n(n- 1)...(n- k + 1)anz n>k

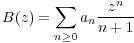
sum zn B(z) = an----- n>0 n + 1

Preuve du lemme :

Preuve du théorème :

Soit 0 < R' < R. S converge en 0, S_N est dérivable sur D(O;R') et z _n>0a_nz^n-k converge normalement sur D(O;R') donc par le théorème de dérivation pour les suites de fonctions, S est dérivable sur D(O;R') et S'(t) = _n>1na_nt^n-1. Par récurrence on montre le résultat à l’ordre k.
Conséquence du téorème d’intégration des suites de fonctions.

Soit sum _n>0a_ntⁿ une série entière réelle de rayon de convergence R > 0 et de somme S(t). Pour tout entier n, le coefficient a_n est égal à 1
n! Sⁿ(0).

Preuve :

clair

3 Développement en série entière

Soit f une application définie sur un ouvert _O_ de et à valeurs dans . On dit que f est développable en série entière en un point t₀ de _O_ s’il existe une série entière sum _n>0a_ntⁿ et un réel > 0 tels que :

oo sum A t (- ]t0- r;t0 +r[, f(z) = an(t -t0)n n>0

Soit _O_ un ouvert de contenant 0 et f infiniment dérivable sur _O_ . La série entière sum _n>0⁺ 1-
!n f⁽ⁿ⁾(0)tⁿ est appelée série de Taylor de f en 0.

Si f est développable en série entière au voisinage de 0, alors f est de classe C à l’origine et la série entière égale à f au voisinage de 0 est nécessairement la série de Taylor de f. Autrement dit,

oo sum (n) E r > 0, A t (- ]- r;r[, f(t) = f-(0)tn n>0 n!

Preuve :

Découle directement de la conséquence 2.

Remarque :

Même si f est de classe C au voisinage de 0, et même si la série de Taylor de f a un rayon de convergence strictement positif, on ne peut affirmer que f est développable en série entière en 0. Considérer f : x '--> exp(- 1
x2 ).