Soit (fn)n une suite d’applications de X dans E. Pour tout entier N, on définit
l’application SN : X |
On se donne une suite (fn)n d’applications d’un espace de Banach X dans un autre espace de Banach E.
Définition :
Soit (fn)n une suite d’applications de X dans E. Pour tout entier N, on définit
l’application SN : X |
Définition :
On dit que la série de fonctions |
Définition :
On dit que la série de fonctions |
Proposition :
Si une série de fonctions est uniformément convergente, alors elle est simplement convergente. |
Preuve :
Immédiat
Remarque :
Soit  n>0fn une série de fonctions, simplement convergente.
n>0fn une série de fonctions, simplement convergente.
Pour tout N de 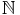 , soit RN =
, soit RN =  n=N+1
n=N+1 f
n le reste d’indice N de cette série.
Dire que la série
f
n le reste d’indice N de cette série.
Dire que la série  n>0fn est uniformément convergente sur X, c’est dire que la
suite (RN)N converge uniformément vers la fonction nulle. Cela équivaut à
écrire :
n>0fn est uniformément convergente sur X, c’est dire que la
suite (RN)N converge uniformément vers la fonction nulle. Cela équivaut à
écrire :

Proposition :
Si |
Preuve :
Pour la convergence uniforme, (fn)n converge uniformément donc (SN)N est de Cauchy uniforme. Par conséquent,

 n > N
n > N  x
x  X ||fn+1(x)||<
X ||fn+1(x)||< 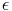 .
.Remarque :
Cette propriété est souvent utilisée pour démontrer qu’une série de fonctions n’est pas uniformément convergente.
Définition :
On dit que la série de fonctions |
Cela revient à dire que la série numérique |
Proposition :
Si une série de fonctions est normalement convergente, alors elle est uniformément convergente et elle est absolument convergente. En particulier, elle est simplement convergente. |
Preuve :
Montrons dans un premier temps que la convergence normale implique la
convergence uniforme. Supposons donc que (fn)n converge normalement sur X.
Il existe une série  n>0
n>0 n convergente avec
n convergente avec  n
n 
 + et ||f
n(x)||<
+ et ||f
n(x)||<  n pour
tout n
n pour
tout n 
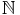 . Alors
. Alors  x
x  X; ||
X; || k=0n+pf
k(x) -
k=0n+pf
k(x) - k=0nf
k(x)||<
||
k=0nf
k(x)||<
|| k=n+1n+pf
k(x)||<
k=n+1n+pf
k(x)||< k=n+1n+p||f
k(x)||<
k=n+1n+p||f
k(x)||< k>n+1||fk(x)||<
k>n+1||fk(x)||< k>n+1
k>n+1 n
qui tend vers 0 quand n tend vers +
n
qui tend vers 0 quand n tend vers + comme reste de la somme d’une série
convergente. Par conséquent, la suite satisfait au critère de Cauchy uniforme et
est donc uniformément convergente.
comme reste de la somme d’une série
convergente. Par conséquent, la suite satisfait au critère de Cauchy uniforme et
est donc uniformément convergente.
Remarque :
La réciproque est fausse.
Proposition :
Soient (fn)n et (gn)n deux suites de fonctions de I dans |
Preuve :
Découle directement des propriétés des limites de suites de fonctions.
Proposition :
Soit (fn)n une suite de fonctions de X dans E. |
On suppose que la série
|
Preuve :
Découle directement des propriétés des limites de suites de fonctions.
Remarque :
Les deux propriétés précédentes peuvent parfois être utilisées pour montrer qu’une série de fonctions n’est pas uniformément convergente.
Proposition :
Soit (fn)n une suite de fonctions d’un intervalle I = [a; b] compact dans
E continues sur X On suppose que la série 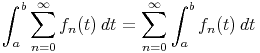 |
Proposition :
Soit (fn)n une suite de fonctions d’un intervalle I de
Alors on a les résultats suivants :
|