On considère dans ce qui suit un 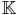 -espace vectoriel normé (E;
-espace vectoriel normé (E;  ).
).
On considère dans ce qui suit un 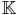 -espace vectoriel normé (E;
-espace vectoriel normé (E;  ).
).
Définition :
Une partie A de E est dite compacte ssi toute suite d’éléments de A admet une valeur d’adhérence dans A. |
Exemple :
Soit (xn)n une suite convergente vers une limite l dans E.
Alors {xn/n 
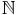 }
}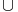 {l} est une partie compacte de E.
{l} est une partie compacte de E.
Proposition :
Une partie A de E est compacte ssi de tout recouvrement de A par des ouverts, on peut extraire un recouvrement fini. |
Proposition :
Preuve :
Soit A une partie compacte de E.  x
x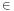 AB(x; 1) est sans aucun doute un
recouvrement de A par des ouverts. On peut donc en extraire un recouvrement
fini, soit
AB(x; 1) est sans aucun doute un
recouvrement de A par des ouverts. On peut donc en extraire un recouvrement
fini, soit  i
i  {1; ...; k}B(xi; 1) qui est donc borné. A est donc incluse dans une
partie bornée, elle est donc elle-même bornée.
{1; ...; k}B(xi; 1) qui est donc borné. A est donc incluse dans une
partie bornée, elle est donc elle-même bornée.
Soit x un élément de l’adhérence de A. Il existe donc une suite (xn)n d’éléments de A qui converge vers x. Or A est compact donc cette même suite a donc une valeur d’adhérence dans A. Toute suite convergente admet pour unique valeur d’adhérence sa limite, x est donc dans A ce qui montre que l’adhérence de A est incluse dans A et par suite que A est égale à son adhérence donc est fermée.
Proposition :
Preuve :
Soit (xn)n une suite d’éléments de Y . Puis que Y est incluse dans X qui est compacte, la suite admet une valeur d’adhérence x dans X. Mais comme Y est fermée, Y est égale à son adhérence et donc x appartient à Y ce qui montre que Y est compacte.
Proposition :
Preuve :
On supposera que N est la norme définie pour tout x = (x1; x2; ...; xk) par
N(x) = max i {1;...;k}Ni(xi)} mais le même type de démonstration resterait
valable pour d’autres normes.
{1;...;k}Ni(xi)} mais le même type de démonstration resterait
valable pour d’autres normes.
Supposons que tous les Ei sont compacts. Soit (xn)n une suite de E. On a donc
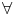 n
n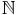 , xn = (0; ...; 0; xni; 0; ...; 0). La suite (x
ni)
n est une suite de Ei pour tout
i
, xn = (0; ...; 0; xni; 0; ...; 0). La suite (x
ni)
n est une suite de Ei pour tout
i  {1; ...; k}.
{1; ...; k}.
Proposition :
Une suite bornée de E est convergente ssi elle n’admet qu’une seule valeur d’adhérence. |
Preuve :
La condition nécessaire est évidente. Soit (xn)n une suite bornée et admettant une unique valeur d’adhérence a. Supposons que (xn)n ne converge pas vers a. Alors :
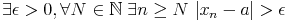
 :
: 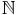

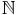 strictement croissante. Pour
N = 0,
strictement croissante. Pour
N = 0,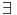 k > N / |xk - a| >
k > N / |xk - a| > 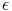 . On pose
. On pose  (0) = k. Supposons construite pour
tout k
(0) = k. Supposons construite pour
tout k  {1; ...; n},
{1; ...; n},  (k) telle que
(k) telle que  (k) >
(k) >  (k - 1) et |x
(k - 1) et |x (k) - a| >
(k) - a| > 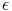 . Alors pour
. Alors pour
 (n);
(n); 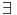 l >
l >  (n) |xl - a| >
(n) |xl - a| > 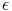 . On pose
. On pose  (n + 1) = l et
(n + 1) = l et  est ainsi construite
jusqu’au rang n + 1. Par récurrence, on construit donc
est ainsi construite
jusqu’au rang n + 1. Par récurrence, on construit donc  strictement croissante
telle que
strictement croissante
telle que 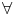 n
n 
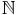 |x
|x (n) - a| >
(n) - a| > 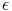 . La suite (x
. La suite (x (n))n est extraite de (xn)n donc
bornée : elle est donc contenue dans un compact et admet donc une valeur
d’adhérence b. b est nécessairement distincte de a car
(n))n est extraite de (xn)n donc
bornée : elle est donc contenue dans un compact et admet donc une valeur
d’adhérence b. b est nécessairement distincte de a car 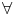 n
n 
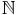 |x
|x (n) - a| >
(n) - a| > 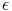 . b
étant une valeur d’adhérence d’une suite extraite de (xn)n, c’est aussi une valeur
d’adhérence de (xn)n ce qui est contraire à l’hypothèse. Donc (xn)n converge
vers a.
. b
étant une valeur d’adhérence d’une suite extraite de (xn)n, c’est aussi une valeur
d’adhérence de (xn)n ce qui est contraire à l’hypothèse. Donc (xn)n converge
vers a.Exemple :
La suite (un)n définie par 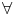 n
n 
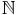 un = (-1)n est bornée, admet deux valeurs
d’adhérence donc ne converge pas.
un = (-1)n est bornée, admet deux valeurs
d’adhérence donc ne converge pas.
Théorème de Heine :
Si f est continue sur un compact [a; b] alors elle est uniformément continue sur [a; b]. |
Preuve :
Supposons que f ne soit pas uniformément continue sur [a; b]. Alors
![E e > 0, A j, E (x;y) (- [a;b]/| x - y |< j et|f(x) - f(y)|> e](compacitehtml3x.gif)
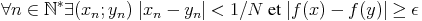
 (n))n qui
converge vers une limite a. (yn)n est aussi une suite de [a; b] compact donc il
existe une suite extraite (x
(n))n qui
converge vers une limite a. (yn)n est aussi une suite de [a; b] compact donc il
existe une suite extraite (x (n))n qui converge vers une limite b. (x
(n))n qui converge vers une limite b. (x o
o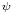 (n))n est
une suite extraite de (x
(n))n est
une suite extraite de (x (n))n donc converge vers a et (y
(n))n donc converge vers a et (y o
o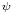 (n))n est une suite
extraite de (y
(n))n est une suite
extraite de (y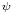 (n))n donc converge vers b. Par continuité de la fonction f,
(f(x
(n))n donc converge vers b. Par continuité de la fonction f,
(f(x o
o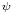 (n)))n tend vers f(a) et (f(y
(n)))n tend vers f(a) et (f(y o
o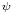 (n)))n tend vers f(b).
(n)))n tend vers f(b).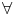 n
n 
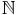 * |x
* |x
 o
o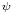 (n) - y
(n) - y o
o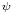 (n)| < 1/N donc
(n)| < 1/N donc
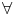
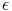 > 0
> 0 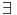 N1
N1 
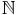
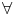 n > N1 |x
n > N1 |x o
o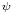 (n) - y
(n) - y o
o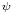 (n)| < 1/N1 <
(n)| < 1/N1 < 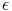 ,
,
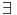 N2
N2 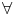 n > N2 |a - x
n > N2 |a - x o
o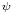 (n)| <
(n)| < 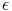 /3 et
/3 et 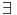 N3
N3 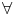 n > N3 |a - x
n > N3 |a - x o
o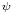 (n)| <
(n)| < 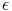 /3. D’où
/3. D’où
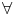 n > maxN1; N2; N3,|a - b| <
|a - x
n > maxN1; N2; N3,|a - b| <
|a - x o
o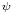 (n)| + |x
(n)| + |x o
o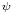 (n) - y
(n) - y o
o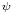 (n)| + |x
(n)| + |x o
o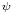 (n) - b| <
(n) - b| < 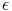 . Puisque a = b, on a donc
f(a) = f(b) donc
. Puisque a = b, on a donc
f(a) = f(b) donc 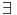 N1/
N1/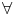 n > N,|f(a) - f(y
n > N,|f(a) - f(y o
o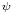 (n))| <
(n))| < 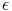 /2 et
/2 et
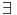 N2,
N2,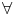 n > N2,|f(a) - f(x
n > N2,|f(a) - f(x o
o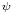 (n)| <
(n)| < 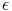 /2. Par conséquent, pour tout
n > max(N1; N2),|f(y
/2. Par conséquent, pour tout
n > max(N1; N2),|f(y o
o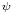 (n)) - f(x
(n)) - f(x o
o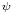 (n))| <
(n))| < 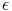 , contrairement à l’hypothèse
de départ. D’où, f est uniformément continue sur [a; b].
, contrairement à l’hypothèse
de départ. D’où, f est uniformément continue sur [a; b].Exemple :
x x2 est uniformément continue sur tout intervalle [a ;b] mais ne l’est pas sur
x2 est uniformément continue sur tout intervalle [a ;b] mais ne l’est pas sur
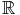 .
.
Théorème :
Preuve :
Soit K un compact et f une fonction continue sur K. Soit (yn)n une suite de
f(K).  n
n 
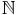 yn = f(xn) où xn
yn = f(xn) où xn  K. (xn)n a une valeur d’adhérence a. Soit
donc (x
K. (xn)n a une valeur d’adhérence a. Soit
donc (x (n))n une sous suite convergente vers a. On a :
(n))n une sous suite convergente vers a. On a :
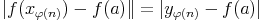

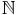 . D’après la continuité de la fonction f, on a :
. D’après la continuité de la fonction f, on a :

 (n))n converge vers f(a).
(n))n converge vers f(a).Théorème :
Preuve :
Soit f une application continue sur un compact K. Alors f(K) est un compact
donc f(K) est bornée.
Soit donc M = sup x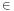 K{f(x)}.
K{f(x)}. 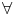 n
n 
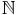 *
* 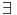 x
n
x
n  K f(xn) > M - (1/n). On a
de manière évidente lim nf(xn) = M.
K f(xn) > M - (1/n). On a
de manière évidente lim nf(xn) = M.
(xn)n est une suite de K donc admet une sous suite (x (n))n convergente vers un
élément l de K.
(n))n convergente vers un
élément l de K.
Par continuité de f, (f(x (n)))n converge vers f(l) mais aussi vers M puisque
(f(x
(n)))n converge vers f(l) mais aussi vers M puisque
(f(x (n)))n est extraite de (f(xn))n. Par unicité de la limite, M=f(l).
(n)))n est extraite de (f(xn))n. Par unicité de la limite, M=f(l).
Même démonstration pour la borne inférieure.
Théorème :
Si f est une bijection continue de [a; b] dans |
Théorème :
Dans un espace vectoriel normé de dimension finie, toutes les normes sont équivalentes. |
preuve (peut être omise en première lecture) :
Soit E un espace vectoriel de dimension finie d et |||| une norme sur E. Il suffit de démontrer qu’elle est équivalente à la norme ||||1.
Soit {e1; e2; ...; en} une base de E.
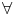 x
x  E,x =
E,x = 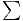 i=1dx
iei on a : ||x|| = ||
i=1dx
iei on a : ||x|| = ||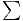 i=1dxiei||<
i=1dxiei||<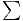 i=1d|x
i|||ei||<
(
i=1d|x
i|||ei||<
(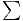 i=1d|x
i|)max{||ei||/i
i=1d|x
i|)max{||ei||/i  {1; ...; d}}.
{1; ...; d}}.
On pose M = max{||ei||/i  {1; ...; d}}. D’où ||x||< M||x||1.
{1; ...; d}}. D’où ||x||< M||x||1.
D’autre part ||||1 est continue sur sur la sphère unité S1 pour la norme ||||1 donc
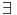 m
m 
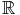 +*/m = inf{||x||
1/x
+*/m = inf{||x||
1/x  S1}.
S1}.
Pour x  E on a alors
E on a alors 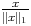
 S1 donc ||
S1 donc ||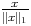 ||> m c’est à dire
||> m c’est à dire 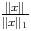 > m et
||x||> m||x||1.
> m et
||x||> m||x||1.
Remarque :
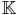 ),
les
normes
||||1
et
||||
),
les
normes
||||1
et
||||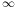 ne
sont
pas
équivalentes.
ne
sont
pas
équivalentes.
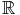 ou
ou
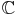 .
.
Par
exemple,
considérons
dans
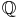 2
considéré
comme
espace
vectoriel
sur
2
considéré
comme
espace
vectoriel
sur
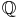 les
deux
normes
N1(r; r') = |r| + |r'|
et
N(r; r') = |r - r'
les
deux
normes
N1(r; r') = |r| + |r'|
et
N(r; r') = |r - r'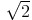 |.
|.
Soit
(an)n
et
(bn)n
deux
suites
d’entiers
naturels
non
nuls
telles
que
la
suite
(an/bn)
converge
vers
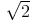 .
.
On
a
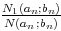 =
= 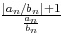 -
-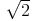 |
qui
tend
vers
+
|
qui
tend
vers
+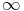 quand
n
tend
vers
l’infini,
ce
qui
montre
qu’il
n’existe
pas
de
constante
k
telle
que
N1 < kN2.
quand
n
tend
vers
l’infini,
ce
qui
montre
qu’il
n’existe
pas
de
constante
k
telle
que
N1 < kN2.
Théorème :
Preuve :
Montrons que toute partie compacte est fermée et bornée. Soit A une partie
compacte de 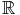 et (un)n une suite d’éléments de A convergente vers un élément a
de
et (un)n une suite d’éléments de A convergente vers un élément a
de 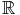 . Alors, toute suite extraite converge vers a. Il existe une suite extraite
(u
. Alors, toute suite extraite converge vers a. Il existe une suite extraite
(u (n))n qui converge dans A puisque A est compact. Mais, comme la suite (un)n
converge vers a, toute suite extraite converge vers a. Donc (u
(n))n qui converge dans A puisque A est compact. Mais, comme la suite (un)n
converge vers a, toute suite extraite converge vers a. Donc (u (n))n converge vers
a ce qui signifie que a est dans A qui est donc fermé.
(n))n converge vers
a ce qui signifie que a est dans A qui est donc fermé.
Si A n’est pas bornée,

 (n))n dans A puisque A est
compacte, la suite (u
(n))n dans A puisque A est
compacte, la suite (u (n))n est donc bornée ce qui est contraire à l’hypothèse
(n))n est donc bornée ce qui est contraire à l’hypothèse
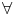 n |u
n |u (n)| >
(n)| >  (n).
(n). et montrons qu’elle est
compacte. Soit donc (xn)n une suite de A. (xn)n est donc bornée. Par le
théorème de Bolzano-Weierstrass, (xn)n a une sous suite convergente et, puisque
A est fermée, la limite de cette sous suite est dans A. On en conclut que A est
compacte.
et montrons qu’elle est
compacte. Soit donc (xn)n une suite de A. (xn)n est donc bornée. Par le
théorème de Bolzano-Weierstrass, (xn)n a une sous suite convergente et, puisque
A est fermée, la limite de cette sous suite est dans A. On en conclut que A est
compacte.Proposition :