 .
.
On considère dans ce qui suit un espace vectoriel E sur un corps  .
.
Proposition et définition :
Soit (Fi)i |
Preuve :
Soit H le sous espace engendré par la réunion des Fi. Si (xi)i I est une famille
presque nulle d’éléments de M telle que
I est une famille
presque nulle d’éléments de M telle que  i
i  I xi
I xi  Fi, alors
Fi, alors
 i
i  I xi
I xi 
 i
i IFi donc
IFi donc  i
i Ixi
Ixi  H par conséquent,
I = {
H par conséquent,
I = { i
i Ixi /
Ixi /  i
i  I xi
I xi  Fi}
Fi} H. D’autre part I est un sous espace
vectoriel qui contient les Fi donc I
H. D’autre part I est un sous espace
vectoriel qui contient les Fi donc I  H. Si J est un sous espace vectoriel
contenant les Fi, il contient I donc I est le plus petit tel et I = H.
H. Si J est un sous espace vectoriel
contenant les Fi, il contient I donc I est le plus petit tel et I = H.
Définition :
Soit (fi)i |
Remarque :
Dans le cas d’une famille finie F1,...,Fn de sous espaces vectoriels de E, on
note F =  i=1nF
i = F1
i=1nF
i = F1  ...
... Fn la somme des Fi si elle est directe. On dit
également dans ce cas que F1, F2,..., Fn sont en somme directe. Tout vecteur v
de F s’écrit alors de manière unique v =
Fn la somme des Fi si elle est directe. On dit
également dans ce cas que F1, F2,..., Fn sont en somme directe. Tout vecteur v
de F s’écrit alors de manière unique v =  i=1nu
i où pour tout i, ui
i=1nu
i où pour tout i, ui  Fi. On
dit que ui est la composante de u sur Fi relativement à cette somme directe.
Fi. On
dit que ui est la composante de u sur Fi relativement à cette somme directe.
Proposition :
Soit (Fi)i |
Preuve :
Si F =  i
i IFi alors
IFi alors  i
i Iui = 0
Iui = 0 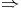
 i
i  I, ui = 0 d’après l’unicité de la
décomposition. Réciproquement, si F =
I, ui = 0 d’après l’unicité de la
décomposition. Réciproquement, si F =  i
i IFi et
(
IFi et
( i
i Iui = 0
Iui = 0 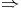
 i
i  I, ui = 0) alors, supposons que x
I, ui = 0) alors, supposons que x  F s’écrive
x =
F s’écrive
x =  i
i Ixi =
Ixi =  i
i Ivi avec xi, vi
Ivi avec xi, vi  I pour tout i
I pour tout i  I. Alors
I. Alors
 i
i I(xi - vi) = 0 donc
I(xi - vi) = 0 donc  i
i  I, xi = vi d’où l’unicité de la décomposition.
I, xi = vi d’où l’unicité de la décomposition.
Proposition :
Soient F et G deux sous espaces vectoriels de E. La somme F +G est directe
ssi F |
Preuve :
Si la somme F + G est directe, soit x  F
F  G et x = x1 + x2 avec x1
G et x = x1 + x2 avec x1  F et
x2
F et
x2  G la décomposition de x. Comme x
G la décomposition de x. Comme x  F , par unicité e la décomposition,
x2 = 0 et de même puisque x
F , par unicité e la décomposition,
x2 = 0 et de même puisque x  G, x1 = 0 donc x = 0. Réciproquement, si
F
G, x1 = 0 donc x = 0. Réciproquement, si
F  G = {0}, soit x
G = {0}, soit x  F + G et x = x1 + x2 = y1 + y2 avec x1, y1
F + G et x = x1 + x2 = y1 + y2 avec x1, y1  F et
x2, y2
F et
x2, y2  G deux décompositions. Alors x1 - y1 = x2 - y2.
x1 - y1
G deux décompositions. Alors x1 - y1 = x2 - y2.
x1 - y1  F
F 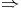 x2 - y2
x2 - y2  F et x2 - y2
F et x2 - y2  G
G 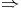 x1 - y1
x1 - y1  G. Donc
x1 - y1
G. Donc
x1 - y1  F
F  G ce qui implique que x1 = y1 et x2 - y2
G ce qui implique que x1 = y1 et x2 - y2  F
F  G qui implique
que x2 = y2.
G qui implique
que x2 = y2.
Proposition :
Si la somme |
Preuve :
Contenue dans la preuve de la proposition précédente.
Remarque :
La réciproque est fausse. Pour montrer que F1,...,Fn sont en somme directe,
avec n > 3, il ne suffit pas de vérifier que pour tous indices i et j distincts,
Fi  Fj = {0}.
Fj = {0}.
Proposition :
Soient F1,...,Fn pour n > 3 des sous espaces vectoriels de E. Alors
la somme F1 + ... + Fn est directe ssi pour tout i |
Définition :
Soient F et G deux sous espaces vectoriels de E. On dit que F et G sont
supplémentaires dans E si E = F |
Théorème :
Soit F un sous espace vectoriel de E. Alors F possède au moins un supplémentaire G dans E. |
Preuve :
Cas où E est de dimension finie n uniquement.
Soit {e1; ...; ep} une base de F , on la complète en une base {e1; e2; ...; en} de E
et on considère G = vect{ep+1; ...; en}. On a de manière évidente E = F  G.
G.
Remarque :
Un même sous espace F de E possède en général une infinité de supplémentaires dans E. Il y a cependant deux cas d’unicité :
Exemple :
 )
des
matrices
carrées
d’ordre
n
à
coefficients
dans
)
des
matrices
carrées
d’ordre
n
à
coefficients
dans
 ,
les
sous
espaces
Sn(
,
les
sous
espaces
Sn( )
et
An(
)
et
An( )
formés
respectivement
des
matrices
symétriques
et
antisymétriques
sont
supplémentaires.
)
formés
respectivement
des
matrices
symétriques
et
antisymétriques
sont
supplémentaires.
 ;
;  )
des
applications
de
)
des
applications
de
 dans
dans
 ,
les
sous
espaces
P(
,
les
sous
espaces
P( ;
;  )
et
A(
)
et
A( ;
;  )
formés
respectivement
des
donctions
paires
et
impaires
sont
supplémentaires.
)
formés
respectivement
des
donctions
paires
et
impaires
sont
supplémentaires.Proposition :
Si p est un projecteur de E (c’est à dire un endomorphisme de E tel que
p o p = p) alors E = Ker(p) |
Preuve :
Soit x  E, alors x = x-p(x) + p(x) avec p(x)
E, alors x = x-p(x) + p(x) avec p(x)  Im(p) et x-p(x)
Im(p) et x-p(x)  ker(p).
En outre, si x
ker(p).
En outre, si x  ker(p)
ker(p)  Im(p), x = p(y) avec y
Im(p), x = p(y) avec y  E et
p(x) = 0 = p o p(y) = p(y) = x.
E et
p(x) = 0 = p o p(y) = p(y) = x.
Proposition :
Si s est un endomorphisme involutif de E (c’est à dire si s o s = id)
alors E = Inv(s) |
Preuve :
Il est évident que Inv(s)  Opp(s) = {0}.
Opp(s) = {0}.
Proposition et définition :
Soit H un sous espace vetoriel de E. Les conditions suivantes sont équivalentes :
Si ces conditions sont réalisées ont dit que F est un hyperplan de E. |
Preuve :
 u
u H,
soit
v
H,
soit
v  E - H.
Alors
v =
E - H.
Alors
v =  u + h
avec
h
u + h
avec
h  H
et
H
et


 *.
On
a
donc
u =
*.
On
a
donc
u =  -1(v - h).
Soit
x
-1(v - h).
Soit
x  E,
alors
x = x1u + x2
avec
x1
E,
alors
x = x1u + x2
avec
x1 
 et
x2
et
x2  H.
D’où
x =
H.
D’où
x =  -1x
1v -
-1x
1v -  -1h + x
2
-1h + x
2 
 v + H.
Par
conséquent,
E =
v + H.
Par
conséquent,
E =  v + H.
Si
x
v + H.
Si
x 
 v
v  H,
x =
H,
x =  v =
v = 
 u +
u +  h.
On
a
donc
h.
On
a
donc

 u +
u +  h
h  H
et
h
H
et
h  H
donc
H
donc

 u
u  H
ce
qui,
puisque
u
H
ce
qui,
puisque
u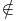 et
et

 0
impose
0
impose
 = 0
et
achève
de
prouver
que
E =
= 0
et
achève
de
prouver
que
E =  v
v  H.
H.
 u
u H,
soit
f
la
forme
linéaire
définie
par
f(
H,
soit
f
la
forme
linéaire
définie
par
f( u + h) =
u + h) =  .
Alors
f
est
une
forme
linéaire
non
nulle
telle
que
ker(f) = H.
.
Alors
f
est
une
forme
linéaire
non
nulle
telle
que
ker(f) = H.
 0.
On
note
H = ker(f).
On
sait
que
H
est
un
sous
espace
vectoriel
de
E.
x
0.
On
note
H = ker(f).
On
sait
que
H
est
un
sous
espace
vectoriel
de
E.
x h.
Soit
u
h.
Soit
u 
 x
x  H.
On
a
u =
H.
On
a
u =  x
avec
x
avec


 *
et
puisque
u
*
et
puisque
u  H,
on
a
f(u) =
H,
on
a
f(u) =  f(x) = 0
d’où
f(x) = 0
d’où
 = 0
et
u = 0.
Soit
y
= 0
et
u = 0.
Soit
y  E.
f(y - f(y)f(x)-1x) = f(y) - f(y)f(x)-1f(x) = 0
donc
y - f(y)f(x)-1x
E.
f(y - f(y)f(x)-1x) = f(y) - f(y)f(x)-1f(x) = 0
donc
y - f(y)f(x)-1x  H
et
y = y - f(y)f(x)-1x + f(y)f(x)-1x
H
et
y = y - f(y)f(x)-1x + f(y)f(x)-1x  H +
H +  x.
Finalement,
E =
x.
Finalement,
E =  x + H.
x + H.Remarque :
Si E est de dimension finie égale à n alors les hyperplans de E sont les sous espaces de E de dimension n - 1.
Proposition :
Les hyperplans de E sont les noyaux des formes linéaires non nulles sur E. |
Proposition :
Deux formes linéaires non nulles sont proportionnelles ssi elles ont le même hyperplan noyau. |
Preuve :
Si f et g sont deux formes linéaires proportionnelles, il existe 

 , f =
, f =  g.
D’où ker(f) = ker(g). Réciproquement, si ker(f) = ker(g), soit u
g.
D’où ker(f) = ker(g). Réciproquement, si ker(f) = ker(g), soit u ker(f).
On a f(u)
ker(f).
On a f(u)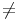 0 et E =
0 et E =  u
u ker(f). Soit x =
ker(f). Soit x =  u + h. On a
f(x) =
u + h. On a
f(x) =  f(u) + f(h) =
f(u) + f(h) =  f(u) donc
f(u) donc  = f(x)f(u)-1 et
g(x) =
= f(x)f(u)-1 et
g(x) =  g(u) + g(h) =
g(u) + g(h) =  g(u) = f(x)f(u)-1g(u). Par conséquent, on a pour
tout x
g(u) = f(x)f(u)-1g(u). Par conséquent, on a pour
tout x  E, g(x) = g(u)f(u)-1f(x), ce qui montre que g et f sont
proportionnelles.
E, g(x) = g(u)f(u)-1f(x), ce qui montre que g et f sont
proportionnelles.