 de dimensions finies n
et m respectivement.
de dimensions finies n
et m respectivement.
On considère deux espaces vectoriels E et F sur un corps  de dimensions finies n
et m respectivement.
de dimensions finies n
et m respectivement.
Définition :
On appelle rang d’une famille {u1; u2; ...; up} de vecteurs de E et on note rg({u1; u2; ...; up}), la dimension du sous espace vectoriel engendré par cette famille. |
Propriétés :
|
Preuve :
Si {u1; ...; up} est libre, c’est une base de < {u1; ldots; up} > donc rg({u1; ...; up}) = p sinon on peut en extraire une base de < {u1; ...; up} donc rg({u1; ...; up}) < p.
Proposition :
Soit f une application linéaire de E dans F . Soit {u1; ...; up} En particulier, si f est bijective, l’égalité est vraie. |
Preuve :
Soit {u1; ...; uq} avec q < p une base de < {u1; ...; up} >, alors {f(u1); ...; f(uq)} est génératrice de < {f(u1); ...; f(up)} > donc rg(< f(u1); ...; f(up) >) < rg({u1; ...; up}) avec égalité ssi (< {f(u1); ...; f(up)} > est libre, ce qui est le cas si f est bijective puisqu’elle transforme toute famille libre en une famille libre.
Définition :
On appelle rang d’une application linéaire f la dimension de Im(f). |
Téorème du rang :
Soit f une application linéaire de E dans F . Alors dim(E)=dim(ker(f))+rg(f). |
preuve :
Soit {u1; ...; ur} une base de ker(f) que l’on complète en une base {u1; ...; un} de E.
Alors {f(u1); ...; f(un)} engendre Im(f) donc {f(ur+1); ...; f(un)} engendre Im(f). En outre, {f(ur+1); ...; f(un)} est libre.
En effet, soit  i, i
i, i  {r + 1; ...; n} tels que
{r + 1; ...; n} tels que  i=r+1n
i=r+1n if(ui) = 0. On a
f(
if(ui) = 0. On a
f( i=r+1n
i=r+1n iui) = 0 donc
iui) = 0 donc  i=r+1n
i=r+1n iui
iui  ker(f).
ker(f).
D’où 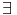
 i
i 
 ,
,  i=1r
i=1r iui =
iui =  i=r+1n
i=r+1n iui.
iui.
Si 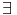 i
i  {r + 1; ...; n} /
{r + 1; ...; n} /  i
i 0, on peut supposer qu’il s’agit de
0, on peut supposer qu’il s’agit de  r+1 et on a alors
ur+1 = -
r+1 et on a alors
ur+1 = - r+1-1
r+1-1 r+2ur+2 - ... -
r+2ur+2 - ... -  n+1-1
n+1-1 nun +
nun +  i=1r
i=1r i
i r + 1-1u
i ce qui est
absurde car la famille {u1; ...; un} est libre.
r + 1-1u
i ce qui est
absurde car la famille {u1; ...; un} est libre.
Par conséquent, {f(ur+1); ...; f(un)} est une base de Im(f) et le résultat s’en déduit.
Propriété :
|
Preuve :
Propriété :
Soient f et g deux endomorphismes de E.
|
Preuve :
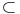 Im(f) + Im(g),
on
a
rg(f + g) < rg(f) + rg(g).
Im(f) + Im(g),
on
a
rg(f + g) < rg(f) + rg(g).
Ecrivant f=(f+g)-g on a alors : rg(f) < rg(f + g) + rg(-g) = rg(f + g) + rg(g) d’où rg(f) - rg(g) < rg(f + g) et le résultat en échangeant f et g.
Si f est injectif, Im(g) et f(Im(g)) sont isomorphes donc rg(f o g) < rg(f). L’inégalité est claire.
Définition :
On appelle rang d’une matrice A Autrement dit, si A = (aij)ij, Ci = (a1i a2i ...; ani) est le i-ème vecteur colonne de A et rg(A) = vect({C1; C2; ...; Cn}. |
Théorème :
rg(A) = rg(tA), c’est à dire si L i = (ai1 ai2 ...aim) est le i-ème vecteur ligne de A, alors rg(A) = vect({L1; ...; Lm}). |
Propriété :
Soit A
|
Propriété :
Soient A,B 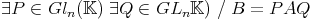 |
Théorème :
Soit A |