Dimension d’un espace vectoriel admettant une famille génératrice finie. Rang d’une application linéaire. Cour de premier cycle universitaire.

F.Gaudon

2 août 2005

Table des matières

1 Familles libres, génératrices, bases
1.1 Sous espace vectoriel engendré
1.2 Familles génératrices, libres
1.3 base
2 Espaces vectoriels de dimension finie
3 Dimension finie et applications linéaires

On considère dans ce qui suit un espace vectoriel E sur un corps .

1 Familles libres, génératrices, bases

1.1 Sous espace vectoriel engendré

Proposition et définition :

Soit A une partie de E. On considère l’ensemble F des combinaisons linéaires d’éléments de A c’est à dire l’ensemble des ₁x₁ + ₂x₂ + ... + _nx_n / n , x_i A, _i . F est un sous espace vectoriel de E appelé sous espace vectoriel engendré par A.

Preuve :

Vérification immédiate.

Proposition :

F est l’intersection de tous les sous espaces vectoriels de E contenant A. C’est donc le plus petit sous espace vectoriel de E contenant la partie A.

Preuve :

Notons d’abord qu’une intersection de sous espaces vectoriels est encore un sous espace vectoriel. F est un espace vectoriel contenant A donc l’intersection des sous espace vectoriels contenant A est contenue dans F . En outre, si un espace vectoriel contient A, il contient toute combinaison linéaire d’éléments de A donc il contient F . Par conséquent, l’intersection des sous espaces vectoriels contenant A contient F . D’où l’égalité.

1.2 Familles génératrices, libres

Définition :

On dit qu’une famille {u_i}_i I d’éléments de E est génératrice si l’espace vectoriel engendré par {u_i}_iI est E.

Définition :

On dit qu’une famille {u_i}_iI d’éléments de E est libre ou encore que les vecteurs de cette famille sont linéairement indépendants si : pour toute famille (_i)_iI de ^(I), sum _iI_iu_i = ==> i I, _i = 0. Dans le cas contraire, c’est à dire s’il existe une famille (_i)_iI de scalaires non tous nuls, telle que sum _iI_iu_i = , on dit que la famille (u_i)_iI est liée, ou encore que les vecteurs qui la composent sont linéairement dépendants (ou liés).

Remarque :

Une famille de vecteurs est liée ssi l’un des vecteurs qui la compose peut s’écrire comme combinaison linéaire des autres.

Preuve :

Si la famille {u_i}_t I d’éléments de E est liée, il existe une famille de scalaires (_i)_iI non tous nuls telle que sum _iI_iu_i = . Soit k I tel que _k soit non nul. On a alors u_k = sum _iI-{k}_i_k^-1u_i. Réciproquement, Si u_k = sum _iI-{k}_iu_i avec _i pour tout i I -{k} alors on a u_k - sum _iI-{k}_iu_i = qui montre que la famille {u_i}_iI est liée.

Proposition :

Toute sous famille d’une famille libre est libre.
Toute famille contenant les éléments d’une famille génératrice est génératrice.

Preuve :

Vérification immédiate

1.3 base

Définition :

On appelle base de E toute famille libre et génératrice.

Proposition :

La famille {u_i}_iI est une base de E ssi tout vecteur v de E peut s’écrire de manière unique comme une combinaison linéaire des vecteurs u_i.

Preuve :

Si {u_i}_iI est une base de E, alors elle est génératrice donc tout v E s’écrit sous la forme v = sum _iI_iu_i avec _i I pour tout i I et les _i non tous nuls.

Si sum _iI_iu_i est une autre écriture de v alors on a sum _iI(_i - _i)u_i = et puisque la famille est libre, i I, _i - _i = 0 d’où l’unicité de l’écriture.

Réciproquement, si tout vecteur v s’écrit comme combinaison linéaire d’éléments de la famille {u_i}_iI alors la famille est génératrice.

En outre, si sum _iI_iu_i = , par unicité de l’écriture de sous forme de combinaison linéaire des éléments de {u_i}, on a i I, _i = 0.

2 Espaces vectoriels de dimension finie

Définition :

Un espace vectoriel est dit de dimension finie s’il admet une famille génératrice finie.

Théorème :

Soit E un espace vectoriel et soit {e₁; e₂; ...; e_n} une famille de n vecteurs de E.

Si {e₁; e₂; ...; e_n} est génératrice de E alors toute famille contenant plus de n vecteurs est liée.
Si {e₁; e₂; ...; e_n} est libre, alors aucune famille de moins de n vecteurs n’est génératrice de E.

Preuve :

Soit p > n et {w₁; ...; w_p} une famille de p vecteurs. La démonstration se fait par récurrence sur n.

Cette propriété est vraie pour n = 1 car si {w₁; w₂} sont deux vecteurs de l’espace vectoriel engendré par {e₁}, alors il existe 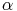et tels que : w₁ = 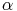e₁ et w₂ = e₁.

Si les deux coefficients sont nuls, alors le système est lié. sinon, on a w₁ - 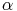w₂ = 0 et le système est lié.

On suppose la propriété vraie pour n - 1 et on la montre pour n. Soit {w₁; w₂; ...; w_p} un système d’un espace vectoriel engendré par {e₁; ...; e_n} avec p > n.

On a dans le sous espace vectoriel engendré par {e₁; e₂; ...; e_n} :

sum n A i (- {1;2;...;n}, wi = akiek k=1

Si tous les a_1i sont nuls, alors les w_i appartiennent en fait au sous espace vectoriel engendré par {e₂; e₃; ...; e_n}. D’après l’hypothèse de récurrence, les w_i forment bien un système lié.

Sinon l’un des a_1i est non nul, par exemple a₁₁. on annule alors la première composante des autres vecteurs, on obtient alors les vecteurs :

w1 a11w2 - a12w1 a11w3 - a13w1 ... a11w1p - a1pw1

Les p - 1 derniers vecteurs sont dans l’espace vectoriel engendré par {e₂; ...; e_n}. Or p - 1 > n - 1 donc l’hypothèse de récurrence s’applique : ils sont liés. Il existe donc _i pour i {2; ...; p} tels que :

c2(a11w2a - a12w1) + c3(a11w3 - a13w1) + ...+ cp(a11w1p - a1pw1 = 0

<==> - (c a + ...+ c a )w + c a w + ...+ c a w = 0 2 12 p 1p 1 2 11 2 p 11 p

On obtient une combinaison linéaire nulle des w_i Le coefficient de w_i pour i {2; ...; n} vaut _ia₁₁ et l’on sait que l’un des _i est non nul et que a₁₁ est non nul donc les coefficients de cette combinaison linéaires sont non tous nuls et par conséquent, le système {w₁; w₂; ...; w_p} est lié.

Le deuxième point est une conséquence directe du premier puisque si une famille de moins de n vecteurs était génératrice, la famille {e₁; ...; e_n} ne serait pas libre d’après le premier point.

Théorème de la base incomplète :

Soit E un -espace vectoriel de dimension finie Soit {e₁; e₂; ...; e_n} une famille génératrice finie de E. Soit {u₁; u₂; ...; u_p} une famille libre de E, non génératrice. Alors il est possible de compléter la famille {u₁; u₂; ...; u_p} à l’aide de vecteurs de la famille {v₁; v₂; ...; v_n} de manière à former une base de E.

Lemme :

Soit E un espace vectoriel sur un corps non réduit à {}. Soit X une famille génératrice de M. Soit A une partie de X non vide et libre. Alors il existe une base B telle que A B X.

Preuve du lemme :

Considérons toutes les parties de X libres et contenant A. Puisque X est fini, elles sont en nombre fini. Parmi elles, on considère celles qui ont un nombre maximal d’éléments. Soit B l’une d’entre elles. On a donc B X, A B et B libre. Notons B = {b₁; b₂; ...; b_n} et montrons que B est génératrice de M. Il suffit de montrer que B est génératrice de X puisque X est génératrice de M. Soit donc x X. Ou bien x B et dans ce cas il n’y a rien à montrer ou bien x / (- B. Dans ce cas, soit B' = B {x} = {b₁; ...; b_n; x}. On a A B' X, B B' et BB' donc B' n’est pas libre. D’où ₁,...,_n, non tous nuls tels ₁b₁ + ... + _nb_n + x = . En particulier 0 sinon ₁b₁ + ... + _nb_n = avec des _i non tous nuls ce qui est impossible car B = {b₁; ...; b_n} est libre. Donc x = -^-1(₁b₁ + ... + _nb_n) ce qui montre que B est génératrice de X.

Preuve du théorème :

Remarquons d’abord que n > p d’après le théorème précédent. {e₁; e₂; ...; e_n} est une famille génératrice donc u₁ = sum _i=1ⁿ_ie_i avec _i . L’un au moins des _i est non nul sinon u₁ serait nul ce qui n’est pas possible car {u₁; u₂; ...; u_p} étant une famille libre, elle ne contient aucun élément nul. Supposons par exemple que ₁0. Alors e₁ = - sum _i=2ⁿ_i₁e_i + u₁ et par conséquent {u₁; e₂; e₃; ...; e_n} est génératrice de E. En outre, u₂ = sum _i=2ⁿ_ie_i + ₁u₁ et l’un au moins des _i pour i {2; ...; n} est non nul sinon on aurait u₂ = ₁u₁ ce qui serait contraire à l’hypothèse {u₁; u₂; ...; u_p} libre. On peut supposer que ₁ est non nul, alors on en déduit que {u₁; u₂; e₃; ...; e_n} est génératrice de E. Et on réitère le procédé. Comme p < n, on a finalement E engendré par {u₁; u₂; ...; u_p; e_p+1; e_p+2; ...; e_n}.

Conséquence :

Tout espace vectoriel de dimension finie non réduit à {} possède une base.

Preuve :

En effet, s’il est de dimension finie, il possède une famille génératrice et puisqu’il n’est pas réduit à {} il possède un vecteur non nul qui forme donc une famille libre que l’on peut compléter en une base.

Théorème :

Si E est un espace vectoriel de dimension finie non réduit à {}, toutes les bases de E ont le même nombre de vecteurs.

Preuve :

Soient {v₁; v₂; ...; v_n} et {w₁; w₂; ...; w_p} deux bases. Alors {v₁; v₂; ...; v_n} est génératrice et {w₁; w₂; ...; w_p} est libre donc p < n. En outre, {v₁; v₂; ...; v_n} est libre et {w₁; w₂; ...; w_p} est génératrice donc n < p. Par conséquent n = p.

Définition :

Le nombre d’éléments que possède une base de E est appelé dimensiondimension de E et noté dim E. Par convention, dim {0} = -.

Théorème de la base incomplète :

Soit un espace vectoriel de base {v₁; v₂; ...; v_n} et soit {w₁; w₂; ...; w_p} un système libre. Alors il existe n - p vecteurs parmi les v_i tel que le système constitué de ces n - p vecteurs v_i et des w_i forment une de E.

Proposition :

Soit E un espace vectoriel de dimension finie n > 1. Soit X={u₁; u₂; ...; u_n} une famille de n éléments de E. Alors {u₁; u₂; ...; u_n} est une base ssi elle est libre ssi elle est génératrice.

Preuve :

Toute base est évidemment une partie libre et génératrice, il suffit donc de montrer que si X est une partie libre alors c’est une base et que si X est génératrice, alors c’est une base. Si X est une partie libre, comme E est de dimension finie et admet donc une famille génératrice, d’après le théorème de la base incomplète, il existe une base B de E contenant X. Mais comme dim E=n=card(X), B et X ont donc le même nombre d’éléments et X B. Par conséquent B = X donc X est une base de E.

Si X est une partie génératrice, X contient un élément non nul x qui forme donc une famille libre {x}. Par le théorème de la bse incompète, on peut compléter {x} en une base B à l’aide de vecteurs de la famille X. On a alors B X. Mais card B=card X donc B=X et par conséquent X est une base de E.

Remarque :

Toute famille de plus de n vecteurs est liée.
Si une famille a moins de n vecteurs,a lors elle n’est pas génératrice.
La dimension de E est donc le nombre maximum d’éléments d’une famille libre ou encore le nombre minimum d’éléments d’une famille génératrice.

Proposition :

Soit F un espace vectoriel d’un espace vectoriel E de dimension finie. Alors F est de dimension finie et dim F<dim E. Si dim E =dim F , alors E = F .

Preuve :

Soit X une base de E c’est donc une famille génératrice finie de E qui est évidemment génératrice de F , sous espace vectoriel de E donc F est de dimension finie. En outre comme de X on peut extraire une base de F on a dim F<dim E. Si dim E= dim F , soit X une base de F , c’est donc une partie libre de F donc de E contenant dim E éléments et par conséquent c’est une base de E.

Remarque :

Sous espace vectoriel de dimension 1 : droite vectorielle
Sous espace vectoriel de dimension 2 : plan vectoriel
Sous espace vectoriel de dimension n - 1 : hyperplan vectoriel

3 Dimension finie et applications linéaires

Proposition :

Soient E et F deux espaces vectoriels sur , E étant de dimension finie. Alors E et F sont isomorphes ssi F est de dimension finie et dim F =dim E.

Preuve :

Définition :

On appelle rang d’une application linéaire f d’un espace vectoriel E dans un autre espace vectoriel F la dimension du sous espace vectoriel Im(f).

Proposition :

rg(f) < n avec égalité ssi f est injective.
rg(f) < m avec égalité ssi f est surjective.
Soit ^*, rg(f) = rg(f).

Proposition :

Soient f et g deux endomorphismes de E.

|rg(f) - rg(g)|< rg(f + g) < rg(f) + rg(g)
rg(fog) < min(rg(f); rg(g)). En outre, si g est surjectif alors rg(fog)) = rg(f) et si f est injectif rg(f o g) = rg(g).

Théorème du rang :

Soient E et F deux espaces vectoriels sur , E étant de dimension finie. Soit f une application linéaire de E dans F . Alors Im(f) est un sous espace vectoriel de dimension finie de F et on a : dim E=rg(f)+dim(Ker(f)).

Proposition :

Soient E et F deux espaces vectoriels de même dimension n et f une application linéaire de E dans F . Alors f est un isomorphisme ssi f est injective ssi f est surjective.