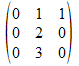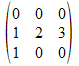Cliquer sur la ou les bonnes réponses.

1. Soit f une application linéaire d'un espace vectoriel E dans un espace vectoriel F.
   
   

   1. Si f est injective alors, pour toute famille génératrice {e_i}_i de E, alors {f(e_i)} est génératrice de F.
      
   2. S'il existe une famille génératrice {e_i}_i de E telle que la famille {f(e_i)_i est génératrice de F, alors f est surjective.
      
   3. Si f est injective, alors pour toute famille {e_i}_i libre de E, {f(e_i)}_i est une famille libre dans F.
      
   4. Si f est surjective, alors pour toute famille {e_i}_i génératrice de E, alors {f(e_i)}_i est génératrice de F
   Correction

2. Soient E et F deux espaces vectoriels de dimensions finies n et p respectivement.
   On désigne par L(E;F) l'espace vectoriel des applications linéaires de E dans F et par L(E) l'espace vectoriel des endomorphismes de E.
   Alors :
   Alors :
   

   1. L(ExF) est isomorphe à L(E)xL(F).
   2. L(E;F) est isomorphe à L(E)xL(F).
   3. L(ExF) est de dimension (n+p)².
   4. L(ExF) est de dimension np.
   5. L(ExF) est de dimension n+p.
   Correction

3. On considère l'endomorphisme f de R³ qui, au triplet (x;y;z) de R³ associe le triplet (4x-5y-5z;5x-6y-7z;-2x+2y+3z).
   Quelle est la matrice de f dans la base canonique de R³ ?
   (d'après école de l'air 2004)

   1. 
      
      
   2. 
      
      
   3. 
      
      
   4. 
      
      
   Correction

4. Soient E et F deux espaces vectoriels sur un corps K. Soient f et g deux morphismes de E dans F tels qu'il existe un endomorphisme de E vérifiant g = f o h.
   Alors :
   
   Que peut-on affirmer ?
   

   1. Im(g) est inclus dans Im(f).
      
   2. Im(f) est inclus dans Im(g).
   3. ker(g) est inclus dans ker(f).
   4. ker(f) est inclus dans ker(g).
   Correction

5. Soit E un espace vectoriel sur un corps K. On considère un projecteur p c'est à dire un endomorphisme de E tel que pop=p.
   Trouver les affirmations vraies parmi les affirmations suivantes :
   

   1. p(x)=0 si x appartient à Im(p).
   2. p(x)=x si x appartient à Im(p).
      
   3. La somme de ker(p) et de Im(p) est directe et égale à E.
      
   4. L'intersection de ker(p) et de Im(p) est réduite à {0}.
   Correction

6. Déterminer la ou les affirmation(s) vraies parmi les affirmations qui suivent concernant la linéarité d'une application u de C dans C :
   
   

   1. Si u est la conjugaison dans C, u est R linéaire.
   2. Si u est la conjugaison dans C, u est C linéaire.
   3. Si u est définie par u(z)=Re(z), u est R linéaire.
      
   4. Si u est définie par u(z)=Re(z), u est C linéaire.
   Correction

7. Soit f l'application linéaire de R dans R³ définie par f(x)=(x;3x;-x).
   Donner la matrice de f dans les bases canoniques de R et R³ :
   

   1.   ?    
   2.   ?    
   3.   ?    
   4.   ?    

8. Donner la matrice dans la base canonique de R³ de l'application linéaire f définie par f(x;y;z)=(y+z;2y;3y)

   1.   ?    
   2.   ?    
   3.   ?