Géométrie vectorielle et analytique dans l'espace, cours, terminale, spécialité Mathématiques
I - Vecteurs de l'espace
Définition :
À tout couple de points $(A;B)$ de l'espace, on associe le vecteur $\vec{AB}$ tel que si $A$ et $B$ ne sont pas confondus, dans un plan qui contient $A$ et $B$, $\vec{AB}$ est le vecteur de la translation qui transforme $A$ en $B$.
Si $A$ et $B$ sont confondus, le vecteur $\vec{AA}$ est le vecteur nul noté $\vec{0}$.
Propriété :
- Pour tout point $A$ de l'espace et pour tout vecteur $\vec{u}$, il existe un unique point $B$ tel que $\vec{AB}=\vec{u}$
- $A$, $B$, $C$ et $D$ quatre points de l'espace. $\vec{AB}=\vec{CD}$ si et seulement si $ABDC$ est un parallélogramme (éventuellement aplati)
- Les règles de calculs sur les vecteurs du plan restent valables dans l'espace.
Définition :
Soit $n$ un entier naturel non nul et $k_1$, $k_2$, ..., $k_n$ des nombres réels. Soit $\vec{u_1}$, $\vec{u_2}$,...,$\vec{u_n}$ des vecteurs de l'espace.
Tout vecteur $\vec{v}$ de la forme $\vec{v}=k_1\vec{u_1}+k_2\vec{u_2}+...+k_n\vec{u_n}$ est appelé \emphref{combinaison linéaire} des vecteurs $\vec{u_1}$, $\vec{u_2}$, ..., $\vec{u_n}$.
II - Droites de l'espace et colinéarité
Propriété :
Deux vecteurs $\vec{u}$ et $\vec{v}$ sont colinéaires si et seulement si il existe un réel $k$ tel que $\vec{u}=k\vec{v}$.
Exemple :
On considère un cube $ABCDEFG$ et les points I, J et K tels que I et le centre de la face BCGF, K est le milieu de [HG] et $\vec{BJ}=\frac{1}{4}\vec{BA}$. On va montrer que $(AK)$ et $(IJ)$ sont parallèles.
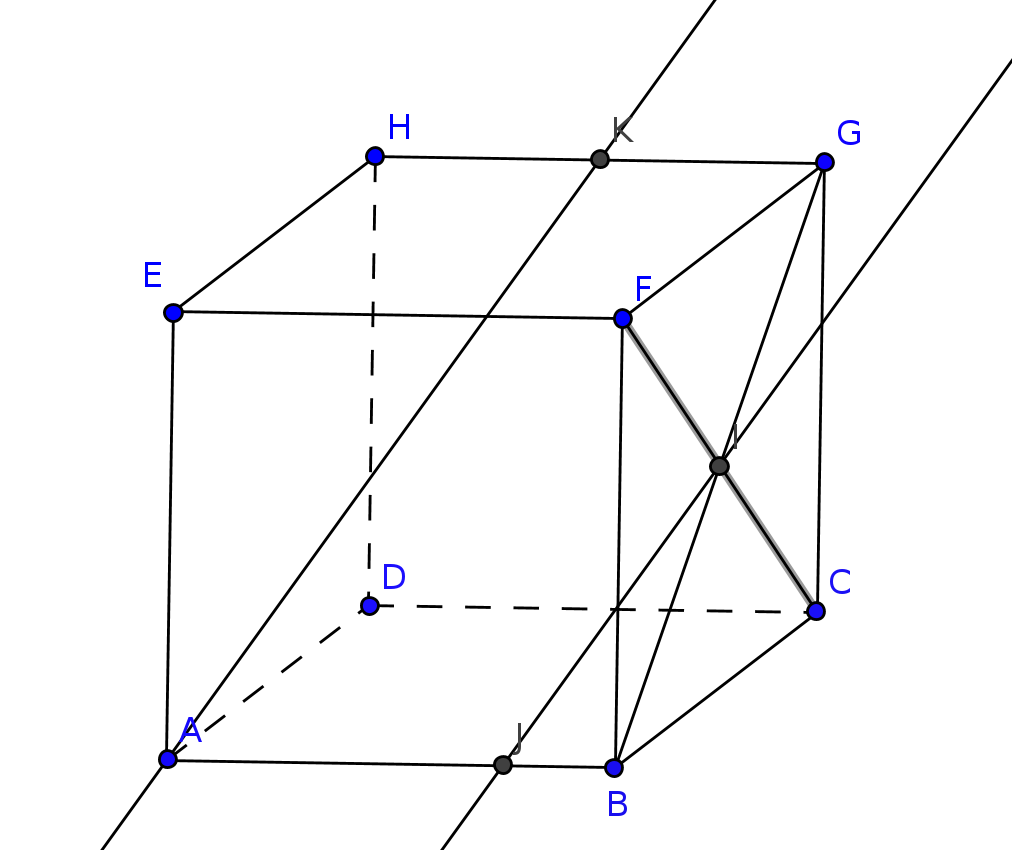
On a $\vec{AK}=\vec{AB}+\vec{BG}+\vec{GK}=\vec{AB}+\vec{BG}-\frac{1}{2}\vec{AB}=\frac{1}{2}\vec{AB}+\vec{BG}$ d'une part et $\vec{JI}=\vec{JB}+\vec{BI}=\frac{1}{4}\vec{AB}+\frac{1}{2}\vec{BG}$ d'autre part. Donc $\vec{AK}=2\vec{JI}$ et les vecteurs $\vec{AK}$ et $\vec{JI}$ sont colinéaires et les droites $(AK)$ et $(IJ)$ sont parallèles.
Définition :
Soient $A$ et $B$ deux points distincts de l'espace. La droite $(AB)$ est l'ensemble des points $M$ de l'espace tels qu'il existe un réel $k$ vérifiant $\vec{AM}=k\vec{AB}$. $\vec{AB}$ est appelé vecteur directeur de la droite.
Propriété et notation :
Une droite $(\mathcal{D})$ de l'espace est définie par un point $A$ et un vecteur directeur $\vec{u}$. On la note $d(A;\vec{u})$.
III - Plans de l'espace et coplanarité
Définition :
$A$, $B$ et $C$ sont trois points de l'espace non alignés. Le plan $(ABC)$ est l'ensemble des points $M$ tels qu'il existe $a$ et $b$ réels vérifiant $\vec{AM}=a\vec{AB}+b\vec{AC}$.
On dit alors que $\vec{AB}$ et $\vec{AC}$ dirigent le plan ou qu'ils sont des vecteurs directeurs du plan $(ABC)$
Propriété et notation
Un plan $(\mathcal{P})$ est défini par un point $A$ et deux vecteurs $\vec{u}$ et $\vec{v}$ non colinéaires. On le note $P(A;\vec{u};\vec{v})$.
Définition :
Trois vecteurs $\vec{u}$, $\vec{v}$ et $\vec{w}$ sont coplanaires si les points $A$, $B$, $C$ et $D$ de l'espace qui vérifient $\vec{u}=\vec{AB}$, $\vec{v}=\vec{AC}$ et $\vec{w}=\vec{AD}$ appartiennent au même plan.
Propriété :
Trois vecteurs $\vec{u}$, $\vec{v}$ et $\vec{w}$ sont coplanaires si et seulement si $\vec{w}$ est combinaison linéaire de $\vec{u}$ et de $\vec{v}$ c'est à dire s'il existe deux réels $a$ et $b$ tels que $\vec{w}=a\vec{u}+b\vec{v}$ ou si $\vec{u}$ et $\vec{v}$ sont colinéaires.
Exemple :
$ABCDEFGH$ est un cube. $I$ est le milieu de $[EF]$. On va montrer que $\vec{GC}$, $\vec{FE}$ et $\vec{AI}$ sont coplanaires :
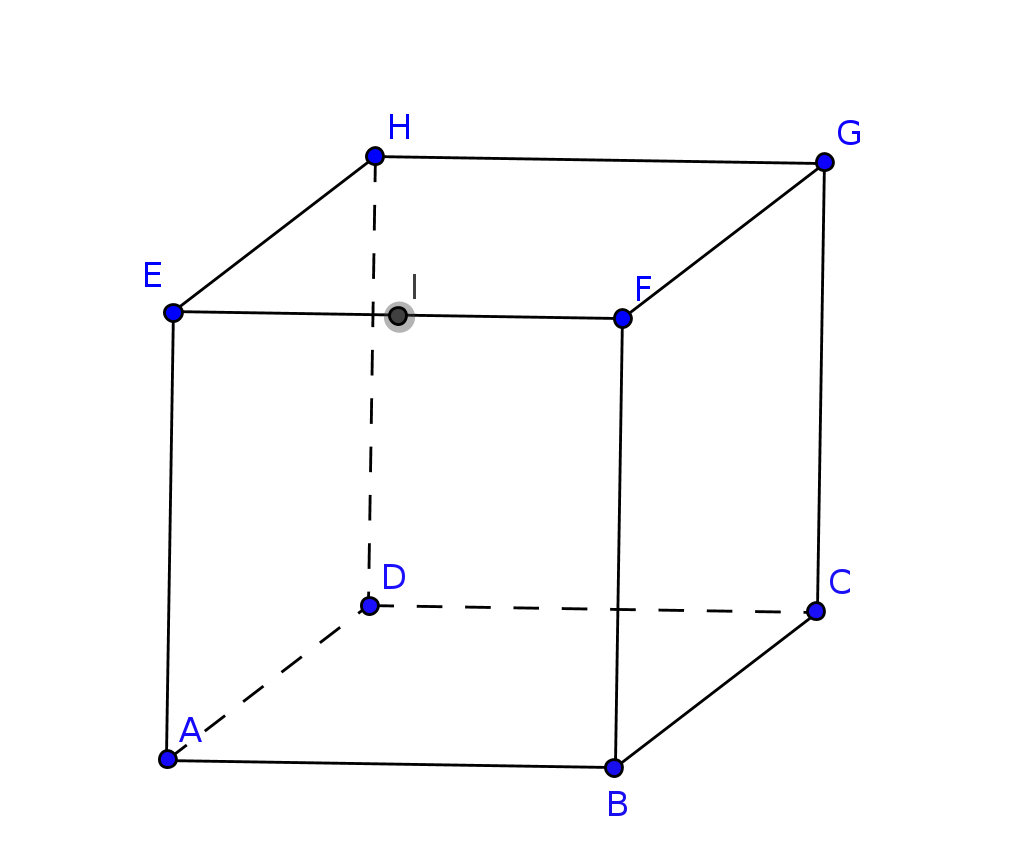
On a $\vec{AI}=\vec{AE}+\vec{EI}=\vec{CG}+\frac{1}{2}\vec{EF}=-\vec{GC}-\frac{1}{2}\vec{FE}$ donc les vecteurs sont coplanaires.
IV - Positions relatives de droites et de plans dans l'espace
1 - Positions relatives entre deux droites
Définition :
Deux droites sont dites coplanaires si elles sont incluses dans le même plan.
Propriété
Soient $(\mathcal{D})$ et $\mathcal{D'}$ deux droites non confondues, c'est à dire distinctes. Les configurations suivantes sont les seules possibles :
Remarque
Deux droites de l'espace non coplanaires n'ont donc aucun point commun et ne sont pourtant pas non plus parallèles, situation qui ne peut se produire dans un plan ou des droites qui n'ont aucun point commun sont parallèles.
2 - Positions relatives entre une droite et un plan
Définition :
Soit $d(A;\vec{u})$ une droite de l'espace et $\mathcal{P}(A;\vec{v};\vec{w})$ un plan de l'espace. La droite $(d)$ est dite parallèle au plan $\mathcal{P}$ si les vecteurs $\vec{u}$, $\vec{v}$ et $\vec{w}$ sont coplanaires.
Propriété :
Une droite est parallèle à un plan si et seulement si elle n'a aucun point commun avec ce plan.
Remarque :
Attention : on a vu précédemment que deux droites qui n'ont aucun point commun ne sont pas nécessairement parallèles.
Propriété :
Une droite $(\mathcal{D})$ de l'espace est parallèle à un plan si et seulement si le plan contient une droite qui lui est parallèle.
Synthèse :
3 - Positions relatives entre deux plans
Définition :
- Deux plans sont dits parallèles si et seulement si deux vecteurs directeurs de l'un peuvent être deux vecteurs directeurs de l'autre.
- Deux plans parallèles sont confondus s'ils ont un point commun.
Propriété :
Deux plans non parallèles sont sécants selon une droite.
Propriété :
Soient $(\mathcal{P})$ et $(\mathcal{P'})$ deux plans distincts. Les configurations suivantes sont les seules possibles :
V - Géométrie analytique dans l'espace
Définition :
- Une base de l'espace est un triplet $(\vec{i};\vec{j};\vec{k})$ de vecteurs non coplanaires.
- Un repère de l'espace est la donnée d'un point origine $O$ et d'une base de l'espace $(\vec{i};\vec{j}; \vec{k})$. On note alors $(O;\vec{i};\vec{j};\vec{k})$ ce repère.
Propriété et définition :
Soit $(\vec{i};\vec{j};\vec{k})$ une base de l'espace. Pour tout $\vec{u}$, il existe un unique triplet $(x;y;z)$ appelé \emphref{coordonnées du vecteur} $\vec{u}$ de réels tels que
$$\vec{u}=x\vec{i}+y\vec{j}+z\vec{k}$$
On note $(x;y;z)$.
Propriété et définition :
Soit $(O;\vec{i};\vec{j};\vec{k})$ un repère de l'espace. Pour tout point $M$ de l'espace, il existe un unique triplet $(x;y;z)$ appelé \emphref{coordonnées du point} $M$ dans le repère $(O;\vec{i};vec{j};\vec{k})$ de réels tels que
$$\vec{OM}=x\vec{i}+y\vec{j}+z\vec{k}$$
$x$ est appelé abscisse de $M$, $y$ est appelé ordonnée de $M$ et $z$ est appelé cote de $M$. On note $M(x;y;z)$.
Propriété :
Soit $(O;\vec{i};\vec{j};\vec{k})$ un repère de l'espace, $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$ deux points.
Alors :
- Le vecteur $\vec{AB}$ a pour coordonnées :
$$\left( \begin{array}{c} x_B-x_A\\ y_B-y_A \\ z_B-z_A \end{array}\right)$$
- le milieu du segment $[AB]$ a pour coordonnées :
$$(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2};\frac{z_A+z_B}{2})$$
- Le centre de gravité du triangle $ABC$ a pour coordonnées :
$$(\frac{x_A+x_B+x_C}{3};\frac{y_A+y_B+y_C}{3};\frac{z_A+z_B+z_C}{3})$$


