Loi binomiale, rappels, cours, classe de TSTMG
Cliquer sur la loupe pour tout révéler ou masquer :
Cliquer sur les ____ pour révéler ou masquer élément par élément.
I - Schéma de Bernoulli
Définition :
Deux expériences sont dites indépendantes si ____le résultat de l'une n'influe pas sur le résultat de l'autre.
Définition :
On considère une expérience aléatoire ne comportant que deux issues ; l'une appelée "succès" et l'autre appelée "échec".
On note $p$ la probabilité de succès et $q$ la probabilité d'échec ($q=1-p$).
La répétition de cette expérience $n$ fois de manière ____indépendante constitue un____ schéma de Bernoulli de paramètres $n$ et $p$.
Propriété :
Dans un schéma de Bernoulli, la probabilité d'une liste de résultats est ____le produit des probabilités de chaque résultat.
Exemple :
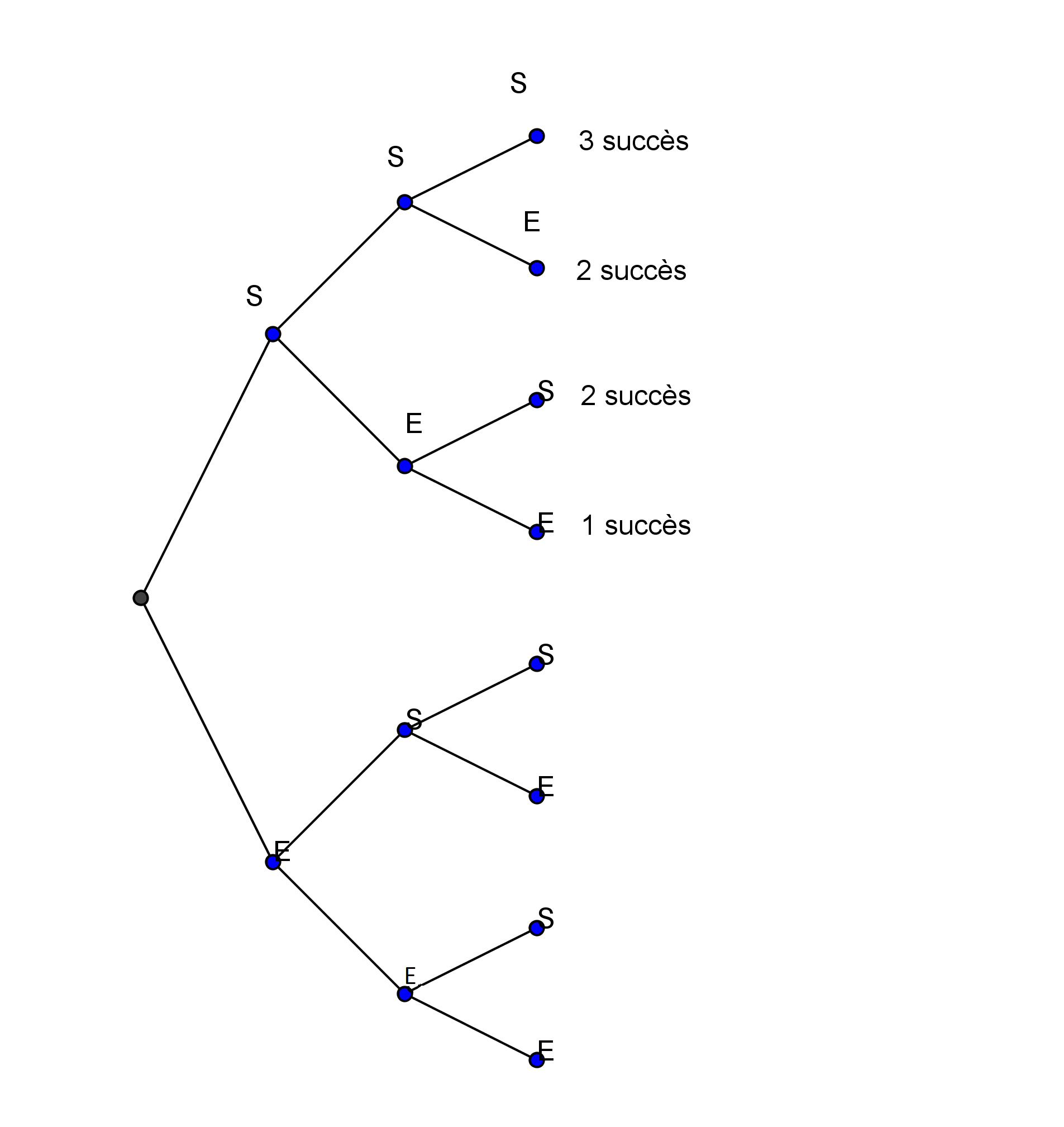
On contrôle la qualité d'un produit sur une chaîne de production. On prélève 3 produits au hasard. On suppose que les prélèvements sont indépendants. Statistiquement, chaque produit a une probabilité $p=0,05$ d'être défectueux.
L'arbre ci-dessus représente un schéma de Bernoulli de paramètres $n=$____3 et $p=$____0,05,
La probabilité d'avoir les deux premières expériences qui donnent un succès et la dernière qui donne un échec est ____$P(SS\bar{S})=0,05^2\times 0,95\approx 0,002$
soit 0,2 \% de chances d'avoir deux produits défectueux sur les trois prélevés.
II - Loi binomiale
Définition :
Soit un schéma de Bernoulli de paramètres $n$ et $p$ et soit $X$ le nombre de succès obtenus. On dit que $X$ est la variable aléatoire associée à ce schéma. On dit aussi que la variable aléatoire $X$ suit une ____loi binomiale de paramètres $n$ et $p$.
Si $k$ est un entier compris entre 0 et $n$, l'événement "on a obtenu $k$ succès" est noté $X=k$ et sa probabilité est notée $P(X=k)$.
Exemple :
On considère le problème précédent de test des produits d'une chaîne de production. Les prélèvements étant supposés indépendants les uns des autres, l'expérience constitue un schéma de Bernoulli de paramètres $n=3$ et $p=0,05$. La variable aléatoire $X$ qui compte le nombre de succès suit la loi binomiale de paramètres $n=3$ et $p=0,05$.
On a $P(X=2)=$____$P(SS\bar{S}\cap S\bar{S}S\cap \bar{S}SS)$
car trois chemins permettent d'obtenir deux succès c'est à dire deux objets défectueux.
D'où ____$P(X=2)=P(SS\bar{S})+P(S\bar{S}S)+P(\bar{S}SS)$
donc ____$P(X=2)=0,05^2\times 0,95+0,95\times 0,05\times 0,95+0,95\times 0,05^2=3\times 0,05^2\times 0,95=0,007$
soit une probabilité très faible de 0,007 d'avoir deux produits défectueux.
Calcul pratique de $P(X=k)$ et $P(X\leq k)$}
Soit $X$ une variable aléatoire de paramètres $n$ et $p$. Pour $k$ allant de 0 à $n$, pour calculer $P(X=k)$ ou $P(X\leq k)$, on utilise une calculatrice :
- Sur Texas instrument : aller dans le menu 2nddistrib, choisir binomFdp et taper n,p,k) pour calculer $P(X=k)$ et choisir binomFRép et taper n,p,k) pour calculer $P(X\leq k)$.
Tutoriel vidéo pour calculatrices TI
- Sur Casio : aller dans le menu STAT puis DIST puis BINM. Sélectionner alors Bpd puis Var pour variable, puis entrer alors $k$ dans la ligne "x", $n$ dans la ligne "numtrial" et $p$ dans la ligne "p" puis aller sur "execute" pour valider et calculer ainsi $P(X=k)$. Pour le calcul de $P(X\leq k)$, on utilisera Bcd au lieu de Bpd.
Tutoriel vidéo pour calculatrices Casio
Exemple :
On considère une variable aléatoire $X$ suivant la loi binomiale de paramètres $n=4$ et $p=0,4$.
Sur TI, la probabilité $P(X\leq 3)$ est donnée par ____binomFrép(4,0.4,3).
Remarques :
- On a $P(X < k)=$____$P(X\leq k-1)$ c'est à dire par exemple $P(X < 3)=$____$P(X\leq 2)$.
- pour calculer $P(X>k)$, on calcule ____$1-P(X\leq k)$. Par exemple, $P(X>2)=$____$1-P(X \leq 2)$.
Définition :
Lorsqu'on simule un "grand nombre de fois" un schéma de Bernoulli de paramètres $n$ et $p$, la moyenne du nombre de succès par schéma se rapproche d'un réel appelé espérance mathématique de la variable aléatoire $X$ que l'on note $E(X)$.
Propriété :
L'espérance mathématique de la loi binomiale de paramètres $n$ et $p$ est :
____$$E(X)=np$$
Exemple :
Pour le problème de la chaîne de production, en prélevant $n=100$ produits indépendamment, la loi binomiale a pour paramètres ____$n=100$ et $p=0,05$.
On a alors $E(X)=$____$np=100\times 0,05=5$ ce qui signifie que l'on peut prévoir ____5 produits défectueux pour un prélèvement de 100 produits indépendants.


