Probabilités conditionnelles, cours, classe de T STMG
Cliquer sur la loupe pour tout révéler ou masquer :
Cliquer sur les ____ pour révéler ou masquer élément par élément.
I - Rappels sur les intersections et les réunions
Définition :
Soient $A$ et $B$ deux événements.
- L'événement $A\cap B$ (lire "$A$ inter $B$") est l'ensemble des issues qui réalisent ____à la fois $A$ et $B$.
- Lorsqu'aucune issue ne réalise $A$ et $B$, c'est à dire $A\cap B=\emptyset$, on dit que $A$ et $B$ sont ____disjoints ou incompatibles.
- L'événement $A\cup B$ (lire "$A$ ou $B$") est l'ensemble des issues qui réalisent ____$A$ ou $B$, c'est à dire au moins un des deux événements.
- L'événement $\bar{A}$ appelé événement ____contraire de $A$ ou complémentaire de $A$ est l'ensemble des issues qui ____ ne réalisent pas $A$.
Propriété :
Soit $P$ une loi de probabilité sur un ensemble $E$.
- Pour tous les événements $A$ et $B$, on a :
____
$$P(A\cup B)=P(A)+P(B)-P(A\cap B)$$
- Pour tout événement $A$,
____
$$P(\bar{A})=1-P(A)$$
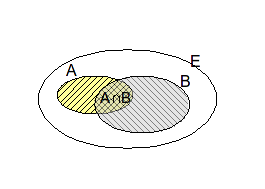
II - Notion de probabilité conditionnelle
Définition :
Pour tout événement $A$ et tout événement $B$ non impossible, on appelle probabilité conditionnelle de $A$ sachant $B$ et notée $P_B(A)$ le nombre
____
$$P_B(A)=\frac{P(A\cap B)}{P(B}$$
Exemple :
Lors d'un sondage, 50\% personnes des interrogées déclarent pratiquer un sport régulièrement et 75\% des
personnes interrogées déclarent aller au cinéma régulièrement. De plus, 40\% des personnes déclarent faire du sport et aller au cinéma régulièrement. On interroge à nouveau une de ces personnes au hasard et on considère les événements \og{}la personne interrogée pratique un sport régulièrement\fg{} et \og{}la personne interrogée va au cinéma régulièrement\fg{} que l'on notent $S$ et $C$ respectivement.
On cherche à calculer la probabilité que la personne pratique un sport régulièrement sachant qu'elle va régulièrement au cinéma.
On a $P(C)=$____$0,75$ et $P(S\cap C)=$____$0,4$.
Donc $P_C(S)=$____$\frac{P(S\cap C)}{P(C)}=\frac{0,4}{0,75}\approx 0,53$.
Remarque :
Soient $A$ et $B$ deux événements non impossibles d'un univers donné. La connaissance de la probabilité d'un événement $B$ et de la probabilité conditionnelle d'un événements $A$ sachant $B$ permet de retrouver la probabilité $P(A\cap B)$ de l'intersection de $A$ et $B$ avec la formule ____$P(A\cap B)=P_B(A)P(B)$.
Exemple :
La tableau suivant montre la répartition du personnel dans une usine :
| Cadres | Ouvriers | Total |
| Hommes | 100 | 200 | 300 |
| Femmes | 50 | 150 | 200 |
| Total | 150 | 350 | 500 |
On rencontre un employé au hasard. On note $H$ l'événement "l'employé rencontré est un homme" et $C$ l'événement "l'employé rencontré est un cadre".
On a $P(H)=$____$\frac{300}{500}=0,6$, $P_H(C)=$____$\frac{100}{300}=\frac{1}{3}$ et $P_H(\bar{C})=$____$\frac{200}{300}=\frac{2}{3}$.
On a bien $P_H(C)+P_H(\bar{C})=$____$1$.
En outre, $P(H\cap C)=$____$P(H)\times P_H(C)=0,6 \times \frac{1}{3}=0,2$
et $P(C)=$____$P(C\cap H)+P(C\cap \bar{H})$.
III - Arbre pondérés

Définition :
Le schéma ci-dessus est appelé arbre pondéré ou arbre à probabilités.
Il comporte 4 chemins :____ $A\cap B$, $A\cap \bar{B}$, $\bar{A}\cap B$ et $\bar{A}\cap \bar{B}$.
Un ____noeud est un point d'où partent plusieurs branches.
Propriété :
Dans un arbre pondéré ou arbre à probabilités comme ci-dessus,
- La somme des probabilités portées sur les branches issues d'un même noeud est égale à ____1 (par exemple, $P_B(A)+P_B(\bar{A})=1$) ;
- la probabilité d'un chemin est ____le produit des probabilités portées par ses branches (par exemple, $P(A\cap B)=P(B) \times P_B(A)$) ;
- la probabilité d'un événement est ____la somme des probabilités des chemins qui le compose(par exemple, $P(A)=P(A\cap B)+P(A\cap \bar{B})$).
Exemple :
 Sur l'arbre ci-dessus :
Sur l'arbre ci-dessus :
- $P_B(A)=$____$0,4$ ; $P_{\bar{B}}(\bar{A})=$____$0,7$ ; $P(B)=$____$0,2$ ;
- $P(\bar{B})=$____$1-P(B)=0,8$ ;
- $P_B(\bar{A})=$____$1-P_B(A)=1-0,4=0,6$ ;
- $P(B\cap A)=$____$P(B)\times P_B(A)=0,2\times 0,4=0,08$ ;
- $P(A)=$____$P(A\cap B)+P(A\cap \bar{B})=0,2\times 0,4+0,8\times 0,3=0,32$.




