Loi binomiale, rappels, cours, classe de TSTMG
Cliquer sur la loupe pour tout révéler ou masquer :
Cliquer sur les ____ pour révéler ou masquer élément par élément.
Etude des lois normales
Définition :
Soit $n$ un entier naturel non nul et $p$ un réel de l'intervalle $[0;1]$.
Lorsque $n$ devient "grand" et si $np>5$ le diagramme en bâton représentant la loi binomiale $X_n$ de paramètres $n$ et $p$ se "rapproche" d'une courbe ayant la forme d'une " cloche".
On dit alors que la variable aléatoire suit une loi normale d'espérance ____ $\mu=np$ et d'écart type ____$\sigma=\sqrt{np(1-p)}$.
Exemple :
Représentation graphique de la loi normale d'espérance $\mu=0$ et d'écart type $\sigma=1$ appelée loi normale ____ centrée réduite.
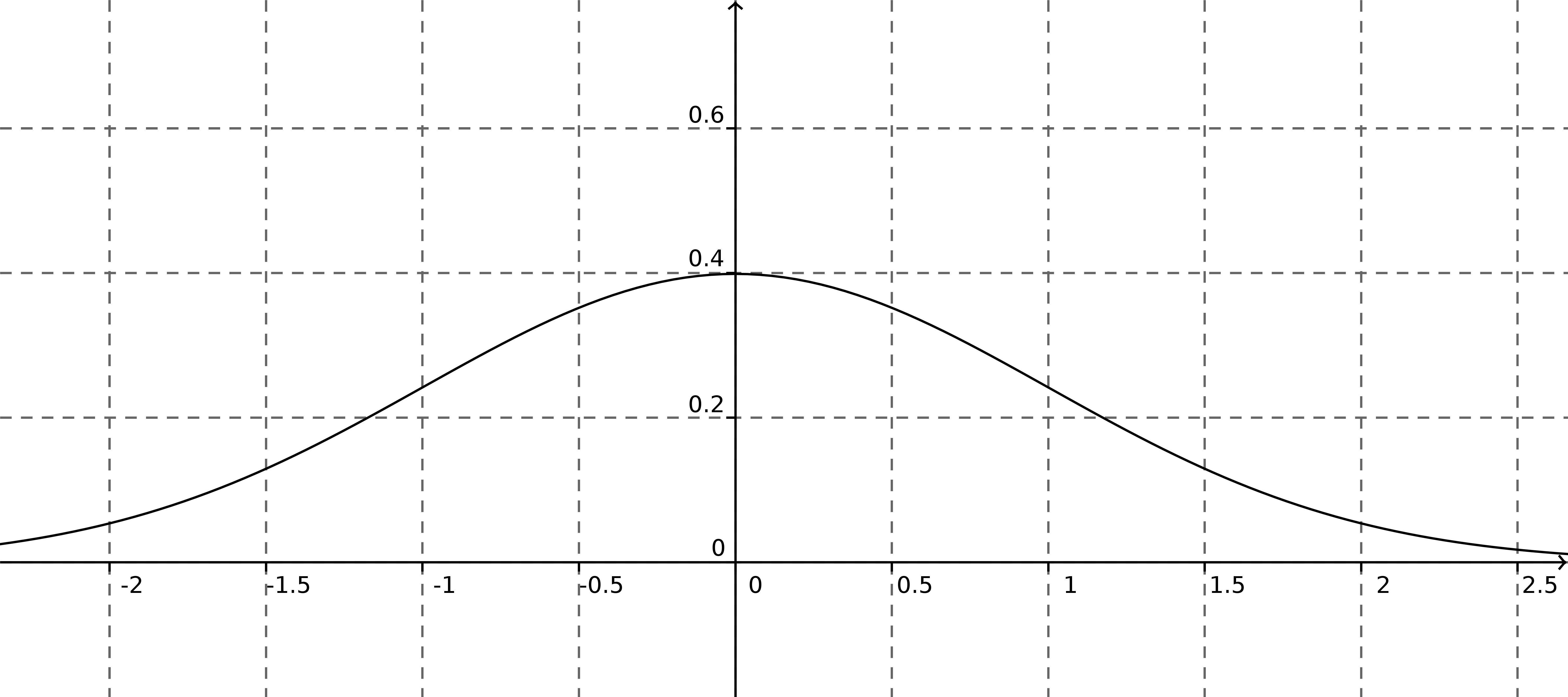
Propriété :
La courbe d'une loi normale est symétrique par rapport à ____la droite parallèle à l'axe $(Oy)$ et d'équation $x=\mu$ où $\mu\in\mathbb{R}$ est l'espérance de la loi normale.
Propriété :
Si $X$ est une variable aléatoire qui suit une loi normale, pour tout réel $b$, la probabilité $P(X\leq b)$ est l'aire de la surface comprise entre ____ la courbe, l'axe des abscisses et à gauche de la droite d'équation $x=b$.
Exemple :
Ci-contre, l'aire correspondante à la probabilité ____$P(X\leq 650)$ pour la loi normale d'espérance ____$\mu=500$ et d'écart type $\sigma=100$.
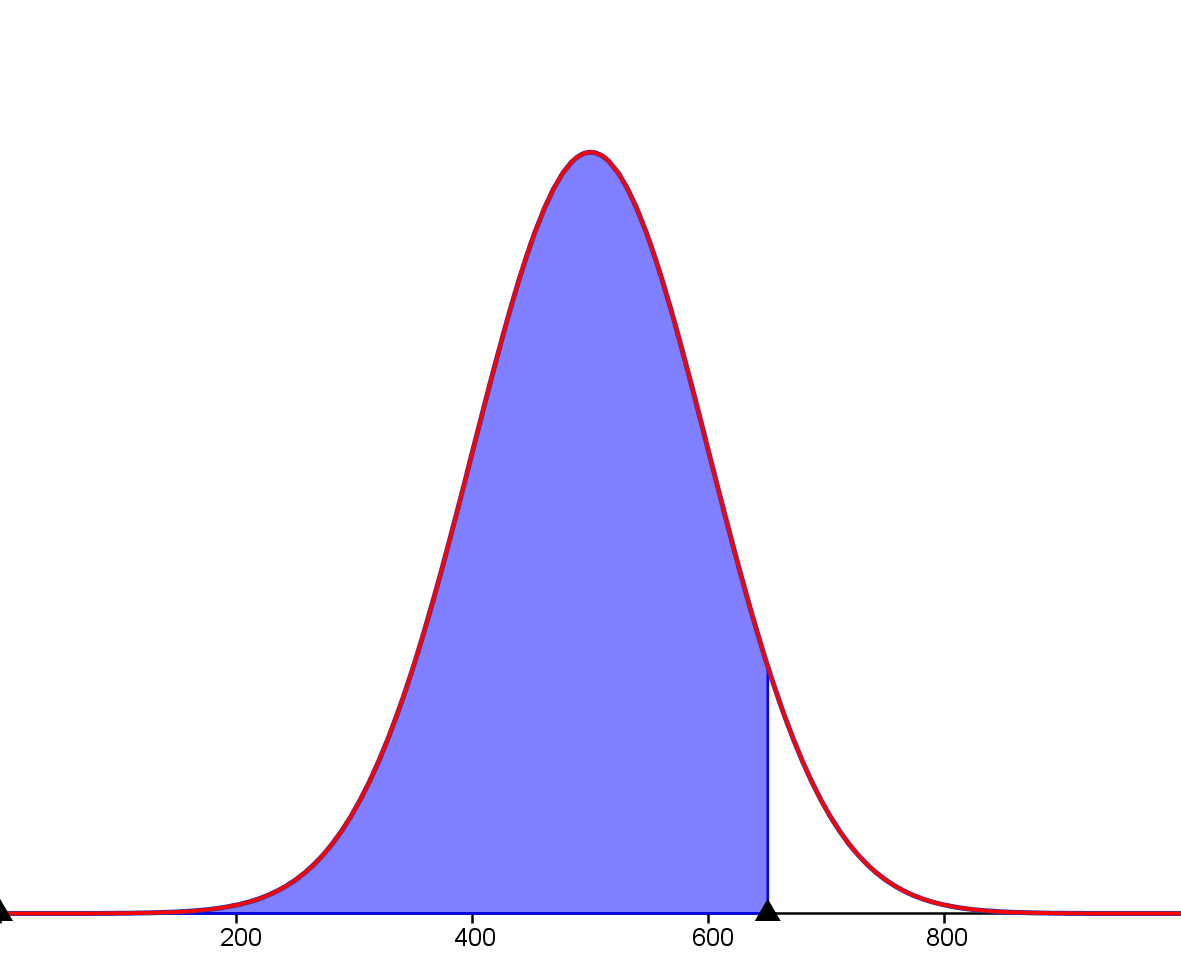
Propriétés :
Soit $X$ une variable aléatoire suivant une loi normale d'espérance $\mu$ et d'écart type $\sigma$.
- L'aire totale comprise entre la courbe et l'axe des abscisses est égale à ____1 ;
- $P(X\leq \mu)=$____$\frac{1}{2}$ c'est à dire que l'aire comprise entre la courbe, l'axe des abscisses et à gauche de la droite d'équation $x=\mu$ est ____$\frac{1}{2}$ ;
- Pour tout réel $b$, $P(X> b)=$____$1-P(X\leq b)$ ;
- Pour tous les réels $a$ et $b$, $P(a\leq X\leq b)=$____$P(X\leq b)-P(X\leq a)$ ;
Utilisation de la calculatrice
Pour calculer $P(a\leq X\leq b)$ :
- Sur Texas Instrument : Dans le menu distrib, sélectionner NormalFrép puis taper $a$,$b$,$\mu$,$\sigma$)
- Sur Casio : Dans le menu STAT choisir DIST puis NORM et ncd puis compléter avec les paramètres $a$, $b$, $\mu$ et $\sigma$.
Propriété :
Si $X$ est une variable aléatoire suivant la loi normale de paramètres $\mu$ et $\sigma$ alors :
____$$P(\mu-2\sigma\leq X\leq \mu+2\sigma)\approx 0,95$$
II - Echantillonnage et estimation
1 - Distinction entre échantillonnage et estimation
Définition :
On considère une population d'individus.
- Lorsque l'on connaît ou lorsque l'on fait une hypothèse sur la proportion $p$ d'individus ayant une caractéristique donnée dans une population et que l'on effectue un nombre $n$ de tirages avec remise dans cette population, la fréquence observée appartient avec une certaine probabilité à un intervalle appelé intervalle de fluctuation de centre $p$ et de longueur qui diminue lorsque $n$ augmente. On parle alors de situation ____d'échantillonnage.
- Lorsque l'on ne connaît pas la proportion d'individus ayant une caractéristique donnée, en procédant à un nombre $n$ de tirages avec remise on peut ____estimer à l'aide de la fréquence $f$ obtenue la proportion $p$ d'individus ayant cette caractéristique. Cette ____estimation se fait à l'aide d'un ____intervalle de confiance dont l'amplitude diminue lorsque le nombre $n$ de tirages augmente.
2 - Echantillonnage
Propriété :
Un intervalle de fluctuation à au moins 95 \% d'une fréquence d'un échantillon de taille $n$ est :
____
$$[p-\frac{1}{\sqrt{n}};p+\frac{1}{\sqrt{n}}]$$
où $p$ est la proportion connue dans la population ou sur laquelle on fait une hypothèse.
Remarque :
En pratique, on utilise cette propriété dès que les conditions $n\geq 30$, $np\geq 5$ et $n(1-p)\geq 5$ sont vérifiées.
Test d'hypothèse :
On considère une population dans laquelle on suppose que la proportion d'un caractère est $p$.On fait l'hypothèse "La proportion dans la population est $p$". On observe la fréquence $f$ d'apparition de ce caractère sur un échantillon de taille $n$ et on calcule l'intervalle de fluctuation $I$ au seuil de 95\%.
- Si $f\notin I$, au risque de 5\% d'erreur (ou au seuil de confiance de 95\%), on ____rejette l'hypothèse que la proportion dans la population est $p$.
- Si $f\in I$, au risque de 5\% d'erreur on ____ne peut pas rejeter l'hypothèse que la proportion dans la population est $p$.
Exemple :
Un fournisseur d'accès à l'internet affirme que, sur sa hotline, seuls 20\% des clients attendent plus de 5 minutes pour obtenir un interlocuteur. Une association de consommateurs interroge au hasard 200 personnes ayant eu à s'adresser à cette hotline. Parmi ces personnes, 53 ont dû attendre plus de 5 minutes. Peut-on mettre en doute l'affirmation du fournisseur d'accès ?\par
L'hypothèse à tester est ____"$p$=20 \% des clients attendent plus de 5 minutes".
____$f=\frac{53}{200}=0,265$
____$I=[0,2-\frac{1}{\sqrt{200}};0,2+\frac{1}{\sqrt{200}}]=[0,129;0,271]$.
Or ____$0,265 \in I$ donc au seuil de confiance de 95\%,____ on accepte l'affirmation du fournisseur d'accès.
Estimation
Propriété et définition :
Soit $p$ la proportion inconnue d'apparition d'un caractère. On appelle $f$ la fréquence d'apparition du caractère sur un échantillon de taille $n$.
Alors, L'intervalle ____$$[f-\frac{1}{\sqrt{n}};f+\frac{1}{\sqrt{n}}]$$
contient pour $n$ assez grand la proportion $p$ avec une probabilité supérieure ou égale à 0,95.
L'intervalle ____$[f-\frac{1}{\sqrt{n}};f+\frac{1}{\sqrt{n}}]$ est appelé intervalle de confiance au niveau de confiance 0,95.
Remarque :
Un intervalle de confiance au niveau de 95\% a une amplitude de ____$\frac{2}{\sqrt{n}}$.
L'amplitude diminue lorsque la taille $n$ de l'échantillon augmente.
Exemple :
Un candidat à une élection municipale fait effectuer un sondage. Sur 100 personnes de la ville interrogées, 63 déclarent vouloir voter pour lui.
____$I=[0,63-\frac{1}{\sqrt{n}};0,63+\frac{1}{\sqrt{n}}]=[0,53;0,73]$
On peut donc estimer que la proportion de personnes dans la ville voulant voter pour lui est comprise dans l'intervalle ____$I=[0,53 ; 0,73]$.



