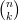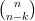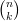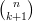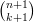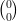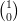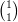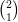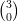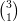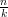p : nombre décimal entre 0 et 1 ;
Début traitement :
t prend une valeur aléatoire décimale entre 0 inclus et 1 exclu ;
si t < p alors
Afficher "Succès" ;
sinon :
Afficher "Échec" ;
Fin Traitement.
Exemple :
| TI :
Prompt P | Casio :
”P”? → P |
| XCas :
saisir("Entrer p : ",p);
t:=alea(0,1); si (t<p) alors afficher("Succès"); sinon afficher("Echec"); fsi;
| Python :
from random import*
p=float(raw_input("Entrer p : ")) t=random() if (t<p): print("Succès") else: print("Echec")
|
2 Coefficients binomiaux
Définition :
| Soit n et k deux entiers naturels tels que k ≤ n. Si n > 0, on appelle factorielle n et on note n! le nombre de permutations de n éléments. On a : 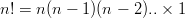 |
Exemple :
Un code est composé de 5 chiffres pris parmi les chiffres de 1 à 5. Il y a 5 × 4 × 3 × 2 × 1 = 5! = 120 codes composés de ces chiffres tous distincts.
Définition et propriété :
| On note 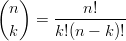 |
Preuve :
Admise
Exemple :
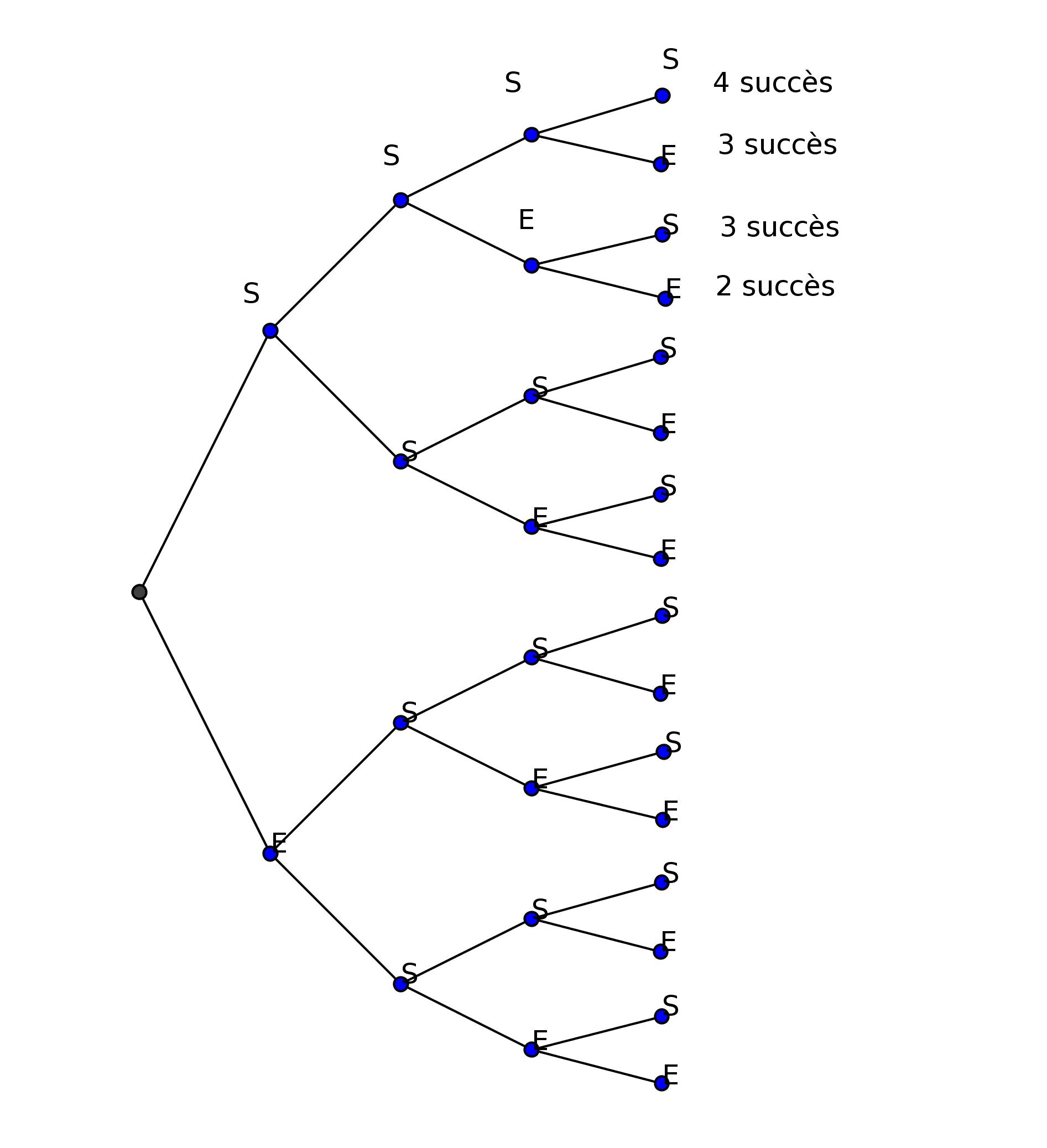
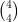 = 1 : il y a une seule manière d’obtenir 4 succès lors de la répétition de 4 épreuves identiques
indépendantes.
= 1 : il y a une seule manière d’obtenir 4 succès lors de la répétition de 4 épreuves identiques
indépendantes.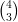 = 4 : il y a quatre manières d’obtenir 3 succès et un échec lors de la répétition de 4 épreuves identiques
indépendantes (SSSE ; SSES ; SESS ;ESSS).
= 4 : il y a quatre manières d’obtenir 3 succès et un échec lors de la répétition de 4 épreuves identiques
indépendantes (SSSE ; SSES ; SESS ;ESSS).
Algorithmique :
Algorithme de calcul de n! pour n entier naturel donné.
Début traitement :
f prend la valeur 1 ;
k prend la valeur de n ;
tant que k > 0 faire :
f prend la valeur de f × k ;
k prend la valeur de k - 1 ;
fin tant que
Fin traitement.
Sortie : f
Exemple :
| XCas :
saisir("Entrer n :",n);
f:=1; k:=n; tantque k>0 faire f:=f*k; k:=k-1; ftantque; afficher("Factorielle :" :f);
| Python :
n=int(raw_input("Entrer n : "))
f=1 k=n while (k>0): f=f*k k=k-1 print("Factorielle :"+f)
|
Propriétés :
|
Preuve :
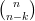 =
= 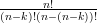 =
= 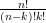
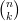 +
+ 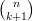 =
= 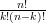 +
+ 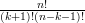 =
= 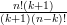 +
+ 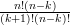
donc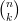 +
+ 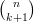 =
= 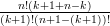 =
= 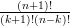 =
= 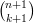 .
.
Triangle de Pascal :
Le triangle de Pascal, du nom de Blaise Pascal, mathématicien français du XVIIe siècle qui le« redécouvra » en Occident (car il était connu avant en Orient et au Moyen-Orient) est une disposition permettant de visualiser et de calculer les coefficients binomiaux et qui s’appuie sur la formule précédente.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
| 3 | 1 |
|
|
| 1 | 4 | 6 | 4 | 1 |
|
| 1 | 5 | 10 | 10 | 5 | 1 |
Explication de la construction : le nombre de la ligne n et de la colonne k est le coefficient binomial 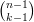 . Il est
obtenu en ajoutant le nombre situé au dessus (ligne n- 1 et colonne k) au nombre de la colonne et de la ligne
précédente (lign n - 1 et colonne k - 1).
. Il est
obtenu en ajoutant le nombre situé au dessus (ligne n- 1 et colonne k) au nombre de la colonne et de la ligne
précédente (lign n - 1 et colonne k - 1).
Par exemple, 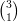 = 3 est la somme de
= 3 est la somme de 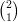 = 2 et de
= 2 et de 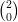 = 1.
= 1.
| 1 | |||||
| 1 | 1 | ||||
| 1 | 2 | 1 | |||
| 1 | 3 | 3 | 1 | ||
| 1 | 4 | 6 | 4 | 1 | |
| 1 | 5 | 10 | 10 | 5 | 1 |
Algorithmique :
Algorithme de construction du triangle de Pascal.
Début traitement :
a est un tableau vide ;
pour k de 0 jusque n faire :
b est un tableau vide ;
pour p de 0 jusque k faire
b[p] prend la valeur 1 ;
fin pour ;
a[k] prend la valeur de b ;
fin pour ;
pour k de 1 jusque n faire :
pour p de 1 jusque k - 1 faire
a[k][p] prend la valeur de a[k-1][p]+a[k-1][p-1] ;
fin pour ;
Afficher a[k] ;
fin pour ;
Fin Traitement.
Exemple :
| XCas :
saisir("Entrer n :",n);
a:=[]; pour k de 0 jusque n faire b:=[]; pour p de 0 jusque k faire b[p]:=1; fpour; a[k]:=b; fpour; pour k de 1 jusque n faire pour p de 1 jusque k-1 faire a[k,p]:=a[k-1,p]+a[k-1,p-1]; fpour; afficher(a[k]); fpour;
| Python :
n=int(raw_input("Entrer n : "))
a=[] for k in range(1,n+2): b=[] for p in range(0,k): b.append(1) a.append(b) for k in range(1,n+1): for p in range(1,k): a[k][p]=a[k-1][1]+a[k-1][p-1] print a[k]
|
3 Loi binomiale
Définition :
| On considère une épreuve de Bernouilli de paramètre p ∈ [0; 1]. On
répète n fois (n ≥ 1) cette expérience indépendamment et on note X la
variable aléatoire qui compte le nombre de succés. On dit alors que la
variable aléatoire X suit une loi binomiale de paramètres n et p et on
note X ~ |
Propriété :
| Si X est une variable aléatoire qui suit une loi binomiale de paramètres
n et p, alors la probabilité d’obtenir k succès avec k ∈{0; 1; 2; ...; n} est
P(X = k) = ( |
Preuve :
Il y a 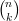 manières d’obtenir k succès dans n répétitions d’expériences identiques et indépendantes. La
probabilité de chacune de ces événements qui sont évidemment incompatibles est pk(1 -p)n-k d’où le résultat.
manières d’obtenir k succès dans n répétitions d’expériences identiques et indépendantes. La
probabilité de chacune de ces événements qui sont évidemment incompatibles est pk(1 -p)n-k d’où le résultat.
Propriété :
| Soit X une variable aléatoire qui suit une loi binomiale de paramètres n et p. Alors :
|
Preuve :
Admise
Algorithmique :
Algorithme de simulation d’une loi binomiale de paramètres n et p.
p : nombre décimal entre 0 et 1 ; n : entier naturel ;
Début traitement : c prend la valeur 0 ;
pour k de 1 jusque n faire :
t prend une valeur aléatoire décimale entre 0 inclus et 1 exclu ;
si t < p alors
c prend la valeur de c + 1 ;
fin si ;
fin pour ;
Fin Traitement.
Sortie : c
Exemple :
| TI :
Prompt N | Casio :
”P”? → P |
| XCas :
saisir("Entrer p : ",p);
saisir("Entrer n : ",n); c:=0; pour k de 1 jusque n faire t:=alea(0,1); si t<p alors c:=c+1; fsi; fpour afficher("Nombre de succès : "+c);
| Python :
from random import*
p=float(raw_input("Entrer p : ")) n=int(raw_input("Entrer n : ")) c=0 for k in range(1,n+1): t=random() if t<p: c=c+1 print("Nombre de succès",c)
|
Algorithmique :
Algorithme de simulation d’obtention de N échantillons de lois binomiales de paramètres n et p.
n, N : nombres entiers ; p : nombre décimal entre 0 et 1 ;
Début traitement :
s est une liste vide ;
pour k de 0 jusque n faire :
s[k] prend la valeur 0 ;
fin pour ;
pour m de 1 jusque N faire :
c prend la valeur 0 ;
pour k de 1 jusque n faire :
t prend une valeur aléatoire décimale entre 0 inclus et 1 exclu ;
si t < p alors :
c prend la valeur de c + 1 ;
fin si ;
fin pour ;
s[c] prend la valeur de s[c] + 1 ;
fin pour ;
Afficher s ;
Fin Traitement.
Exemple :
| XCas :
saisir("Entrer p : ",p);
saisir("Entrer n : ",n); saisir("Entrer N : ",N); s:=[]; pour k de 0 jusque n faire s[k]:=0; fpour; pour m de 1 jusque N faire c:=0; pour k de 1 jusque n faire t:=alea(0,1); si t<p alors c:=c+1; fsi; fpour; s[c]:=s[c]+1; fpour; pour k de 0 jusque n faire afficher("Avec "+k+" succès : "+s[k]); fpour;
| Python :
from random import*
p=float(raw_input("Entrer p : ")) n=int(raw_input("Entrer n : ")) N=int(raw_input("Entrer N : ")) s=[] for k in range(0,n+1): s.append(0) for m in range(1,N+1): c=0 for k in range(1,n+1): t=random() if t<p: c=c+1 s[c]=s[c]+1 for k in range(0,n+1): print "Nombre avec "+k+" succès : "+s[k]
|
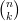 (on dit «
(on dit «