Symetrie centrale cours 5e

Symétrie centrale cours 5e

F.Gaudon

31 décembre 2004

Première approche :

Deux figures sont symétriques par rapport à un point O quand elles se superposent par un demi-tour de centre O.

Définition :

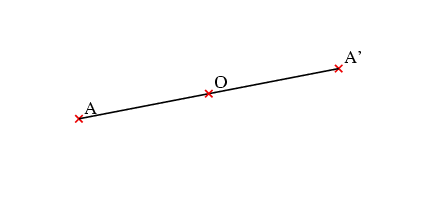
Deux points A et A’ sont symétriques par la symétrie centrale de centre O si O est le milieu du segment [AA’].

Vocabulaire :

A’ est aussi appelé le symétrique de point A par rapport au point O.

Remarque :

Le symétrique d’un point O par la symétrie de centre O est le point O lui-même, on dit que O est son propre symétrique ;

Construction du symétrique A’ d’un point A donné par rapport à un point O donné :

On trace la droite (OA) ;
on place le deuxième point d’intersection du cercle de centre O passant par le point A avec la droite (OA).

Propriétés :

Si deux segments sont symétriques par une symétrie centrale, alors ils ont même longueur ;
si deux angles sont symétriques par une symétrie centrale, alors ils ont même mesure ;
si deux figures sont symétriques par une symétrie centrale, alors elles ont la même aire ;

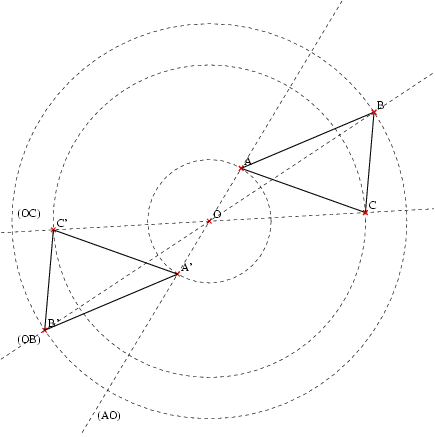
Propriétés :

si deux droites sont symétriques par une symétrie centrale, alors elles sont parallèles ;
si trois points sont alignés, alors leurs symétriques par une symétrie centrale sont alignés.