
Définition :
Deux angles sont adjacents s’ils ont le même sommet, un côté commun et s’ils sont situés de part et d’autre du côté commun. |

Définition :
Deux angles sont opposés par le sommet s’ils ont le même sommet et s’ils sont symétriques par rapport au sommet commun. |

Propriété :
Si deux angles sont opposés par le sommet, alors ils ont même mesure. |
Définition :
Deux angles sont complémentaires si leur somme vaut 90º . |

Définition :
Deux angles sont supplémentaires si leur somme vaut 180º . |

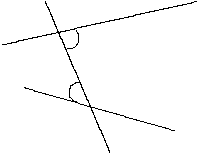
Définition :
Deux angles sont alternes internes s’ils sont situés de part et d’autre d’une droite sécante à deux autres droites et entre ces deux droites. |
Définition :
Deux angles sont correspondants s’ils sont situés du même côté d’une droite sécante à deux autre droites, l’un étant entre les deux droites, l’autre pas. |

Propriété :
|
Preuve :
 en
deux
points
A
et
B.
Soit
I
le
milieu
de
[AB].
Les
deux
points
A
et
B
sont
donc
symétriques
par
rapport
au
point
I.
Le
point
A
appartient
à
la
droite
(d1)
donc
son
symétrique
B
appartient
à
la
droite
symétrique
de
la
droite
(d1)
par
rapport
au
point
I.
D’après
la
propriété
”Si
deux
droites
sont
symétriques
par
rapport
à
un
point,
alors
elles
sont
parallèles
entre
elles”
on
en
déduit
que
la
droite
symétrique
de
(d1)
est
parallèle
à
(d1).
La
droite
symétrique
de
(d1)
est
donc
la
droite
parallèle
à
(d1)
et
passant
par
le
point
B :
c’est
la
droite
(d2).
Par
conséquent,
les
angles
alternes
internes
formés
sont
symétriques
par
rapport
à
I
et
ont
donc
même
mesure.
en
deux
points
A
et
B.
Soit
I
le
milieu
de
[AB].
Les
deux
points
A
et
B
sont
donc
symétriques
par
rapport
au
point
I.
Le
point
A
appartient
à
la
droite
(d1)
donc
son
symétrique
B
appartient
à
la
droite
symétrique
de
la
droite
(d1)
par
rapport
au
point
I.
D’après
la
propriété
”Si
deux
droites
sont
symétriques
par
rapport
à
un
point,
alors
elles
sont
parallèles
entre
elles”
on
en
déduit
que
la
droite
symétrique
de
(d1)
est
parallèle
à
(d1).
La
droite
symétrique
de
(d1)
est
donc
la
droite
parallèle
à
(d1)
et
passant
par
le
point
B :
c’est
la
droite
(d2).
Par
conséquent,
les
angles
alternes
internes
formés
sont
symétriques
par
rapport
à
I
et
ont
donc
même
mesure.
Propriété :
|
Preuve :
 en
deux
points
A
et
B.
En
considérant
l’angle
opposé
à
l’un
des
deux
angles
correspondants
on
obtient
des
angles
alternes-internes.
La
propriété
énoncée
plus
haut
permet
donc
d’affirmer
que
ces
angles
alternes-internes
sont
égaux
et
par
conséquent
que
les
angles
correspondants
le
sont
aussi.
en
deux
points
A
et
B.
En
considérant
l’angle
opposé
à
l’un
des
deux
angles
correspondants
on
obtient
des
angles
alternes-internes.
La
propriété
énoncée
plus
haut
permet
donc
d’affirmer
que
ces
angles
alternes-internes
sont
égaux
et
par
conséquent
que
les
angles
correspondants
le
sont
aussi.
Propriété :
La somme des angles d’un triangle est égale à 180º . |
Preuve :
Soit ABC un triangle, I le milieu de [AB] et J le milieu de [AC]. On
appelle B’ le symétrique de B par rapport à J et C’ le symétrique de C par
rapport à I.
Les points C’, A et B ont donc pour symétriques par rapport à I les points
C, B et A. Par conséquent,  , est le symétrique de
, est le symétrique de  par rapport à
I et donc d’après la propriété ”Si deux angles sont symétriques par rapport
à un point alors ils ont même mesure on en déduit que
par rapport à
I et donc d’après la propriété ”Si deux angles sont symétriques par rapport
à un point alors ils ont même mesure on en déduit que  =
=  . De
plus (AC’) est la droite symétrique de (BC) par rapport à I donc d’après la
propriété ”Si deux droites sont symétriques par rapport à un point, alors
elles sont parallèles” on en conclut que (AC’) et (BC) sont parallèles.
. De
plus (AC’) est la droite symétrique de (BC) par rapport à I donc d’après la
propriété ”Si deux droites sont symétriques par rapport à un point, alors
elles sont parallèles” on en conclut que (AC’) et (BC) sont parallèles.
Les points B’, A et C ont pour symétriques les points B, C et A par rapport
à J. Par conséquent,  et
et  sont symétriques par rapport à J et par
la même propriété que précédemment,
sont symétriques par rapport à J et par
la même propriété que précédemment,  =
=  . En outre, (AB’) et
(BC) sont symétriques par rapport à J donc elles sont parallèles.
. En outre, (AB’) et
(BC) sont symétriques par rapport à J donc elles sont parallèles.
On sait donc que (AC’) et (BC) sont parallèles et que (AB’) et (BC) sont
parallèles donc d’après la propriété ”Si deux droites sont parallèles à une
même troisième, alors elles sont parallèles entre elles”, on en déduit que les
droites (AC’) et (AB’) sont parallèles et comme elles ont le point A en
commun, elles sont confondues. D’où A, B’ et C’ sont alignés.
En outre, on a donc



Propriétés pour les triangles isocèles :
|
Preuve :
 et
et
 sont
symétriques
par
rapport
à
(d).
D’après
la
propriété
”si
deux
angles
sont
symétriques
par
rapport
à
une
droite,
alors
ils
ont
même
mesure”
on
en
déduit
que
sont
symétriques
par
rapport
à
(d).
D’après
la
propriété
”si
deux
angles
sont
symétriques
par
rapport
à
une
droite,
alors
ils
ont
même
mesure”
on
en
déduit
que
 =
=  .
.
 et
et
 égaux.
Soit
I
le
milieu
du
segment
[BC]
et
(d)
la
médiatrice
de
[BC].
On
appelle
A’
l’intersection
de
(d)
avec
(AB).
égaux.
Soit
I
le
milieu
du
segment
[BC]
et
(d)
la
médiatrice
de
[BC].
On
appelle
A’
l’intersection
de
(d)
avec
(AB). a
pour
symétrique
a
pour
symétrique
 par
rapport
à
(d)
et
donc
le
symétrique
A’
lui-même
de
A’
appartient
au
côté
[CA).
A’
appartient
donc
à
[CA)
mais
aussi
par
construction
à
(AB)
donc
A’
est
confondu
avec
A.
Comme
A’
c’est
à
dire
A
appartient
à
la
médiatrice
(d)
de
(BC),
d’après
la
propriété
”Si
un
point
appartient
à
la
médiatrice
d’un
segment,
alors
il
est
à
égales
distance
des
extrémités
d’un
segment”
on
en
déduit
que
AB=AC
c’est
à
dire
ABC
est
un
triangle
isocèle
en
A.
par
rapport
à
(d)
et
donc
le
symétrique
A’
lui-même
de
A’
appartient
au
côté
[CA).
A’
appartient
donc
à
[CA)
mais
aussi
par
construction
à
(AB)
donc
A’
est
confondu
avec
A.
Comme
A’
c’est
à
dire
A
appartient
à
la
médiatrice
(d)
de
(BC),
d’après
la
propriété
”Si
un
point
appartient
à
la
médiatrice
d’un
segment,
alors
il
est
à
égales
distance
des
extrémités
d’un
segment”
on
en
déduit
que
AB=AC
c’est
à
dire
ABC
est
un
triangle
isocèle
en
A.Propriétés pour les triangles équilatéraux :
|
Propriété du triangle rectangle :
Les deux angles aigus d’un triangles rectangle sont complémentaires. |