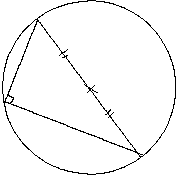
Théorème :
Si un triangle est rectangle, alors son hypoténuse est un diamètre du cercle circonscrit à ce triangle. |
Preuve :
Soit ABC un triangle rectangle en A et O le milieu de l’hypoténuse [BC].
Soit D le point tel que O est le milieu de [AD]. On sait que O est le milieu
de [BC] et que O est le milieu de [AD]. D’après la propriété : ”Si un
quadrilatère a ses diagonales qui se coupent en leur milieu alors c’est un
parallélogramme”, donc ABDC est un parallélogramme.
On sait que ABDC est un parallélogramme et que 
est un angle droit.
D’après la propriété : ”Si un parallélogramme a un angle droit alors c’est un
rectangle” on en conclut que ABDC est un rectangle.
On sait que ABDC est un rectangle. D’après la propriété : ”Si un
quadrilatère est un rectangle, alors ses diagonales se coupent en leur milieu
et sont de même longueur” on conclut que OA = OB = OC. OA = OB
donc d’après la propriété ”Si un point se trouve à égale distance des
extrémités d’un segment, alors il appartient à la médiatrice de ce segment”
on en déduit que O appartient à la médiatrice de [AB]. De même de
OB = OC on déduit que O appartient à la médiatrice de [BC] et de
OA = OC on déduit que O appartient à la médiatrice de [AC]. Par
définition, le centre du cercle circonscrit à un triangle est le point
d’intersection des médiatrices donc O est le centre du cercle circonscrit au
triangle ABC et par suite [BC] en est un diamètre.
Conséquence :
Si un triangle est rectangle, alors le milieu de l’hypoténuse est le centre du cercle circonscrit à ce triangle. |
Propriété :
Si un triangle est rectangle, alors la longueur de la médiane issue de l’angle droit est égale à la moitié de la longueur de l’hypoténuse. |
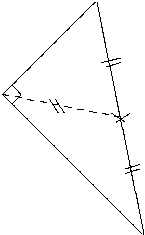
Preuve :
Soit ABC un triangle rectangle en A et O le milieu de l’hypoténuse [BC].
On sait que ABC est un triangle rectangle en A donc d’après la propriété
”Si un triangle est rectangle, alors le milieu de l’hypoténuse est le centre du
cercle circonscrit à ce triangle” on en déduit que O est le centre du cercle
circonscrit au triangle ABC. Par définition, le centre du cercle circonscrit à
un triangle est le point d’intersection des médiatrices des côtés du triangle
donc O est le point d’intersection des médiatrices des segments [AB], [BC]
et [AC]. D’après la propriété ”si un point appartient à la médiatrice d’un
segment, alors il se trouve à égale distance des extrémités d’un segment” on
en déduit que OA = OB, OA = OC et OB = OC c’est à dire que
OA = OB = OC donc OA =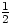 
BC.
Théorème :
Si un triangle inscrit dans un cercle a un diamètre pour côté, alors c’est un triangle rectangle. |
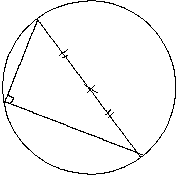
Preuve :
Soit ABC un triangle inscrit dans un cercle C et tel que [AB] est un
diamètre du cercle. on appelle O le centre du cercle et on appelle D le
symétrique de C par rapport à O.
On sait que [AB] est un diamètre du cercle donc que O est le milieu [AB]
et on sait que C et D sont symétriques par rapport à O donc que O est le
milieu de [CD] donc d’après la propriété ”Si un quadrilatère a ses
diagonales qui se coupent en leur milieu alors c’est un parallélogramme ” on
conclut que ADBC est un parallélogramme.
OD = OC donc O est sur le cercle C. On sait donc que
OA = OB = OC = OD d’où d’après la propriété ”si un parallélogramme a
ses diagonales de même longueur alors c’est un rectangle ” on conclut que
ADBC est un rectangle donc que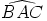 
est un angle droit.
Conséquence :
Si dans un triangle, la médiane issue d’un sommet a pour longueur la moitié de la longueur du côté opposé, alors ce triangle est rectangle. |
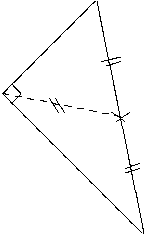
Preuve :
Soit ABC un triangle et [OA] une médiane avec O milieu de [BC]. Par
hypothèse on a donc OA = 
BC et comme O est le milieu de [BC], on a
donc OB = OC d’où finalement OA = OB = OC. On en déduit que O est
le centre du cercle circonscrit C au triangle ABC. Ce triangle ABC est donc
inscrit dans le cercle C et [BC] en est un diamètre. D’après la propriété ”Si
un triangle inscrit dans un cercle a un diamètre pour côté, alors c’est un
triangle rectangle” on en conclut que ABC est un triangle rectangle.