|
|
Définition :
La médiatrice d’un segment est la droite perpendiculaire à ce segment et passant par son milieu. |
Propriétés :
|
|
|
Preuve :
Soit ABC un triangle non aplati et soient (d1), (d2) et (d3) les médiatrices
respectives des côtés [AB], [BC] et [AC].
Puisque le triangle n’est pas aplati, les droites (d1) et (d2) se coupent en un
point O. Il s’agit de montrer que le point O est aussi sur (d3).
On sait que O est sur la médiatrice (d1) de [AB]. D’après la propriété : ”si
un point appartient à la médiatrice d’un segment alors il est à égale
distance des extrémités du segment” on en déduit que OA = OB.
De même, O est sur la médiatrice (d2) de [BC] donc OB = OC.
OA = OB et OB = OC donc OA = OC. D’après la propriété : ”si un point
est situé à égale distance des extrémités d’un segment alors il appartient à
la médiatrice de ce segment”, on en déduit que O appartient à la médiatrice
(d3) du segment [AC], ce qu’il fallait démontrer. 
Définition :
Dans un triangle, les hauteurs sont les droites passant par un sommet et perpendiculaires au côté opposé. |
Propriété :
Les hauteurs d’un triangle sont concourantes en un point appelé orthocentre du triangle. |
|
|
Preuve :
Soit ABC un triangle non aplati. Soit (dA) la hauteur issue de A, (dB) la
hauteur issue de B et (dC) la hauteur issue de C. Soient (d'C) la droite
parallèle à la droite (AB) et passant par le point C, (d'A) la droite parallèle
à la droite (BC) passant par le point A et (d'B) la droite parallèle à (AC)
passant par le point B.
(d'A) et (d'B) se coupent en un point C', (d'B) et (d'C) se coupent en au
point A' et (d'A) et (D'C) se coupent en un point B'.
On va d’abord montrer que (dB) est la médiatrice du segment [A'C'] :
On sait que (A'C) et (AB) sont parallèles et que (A'B) et (AC) sont
parallèles. D’après la propriété : ”si un quadrilatère a ses côtés parallèles
deux à deux alors c’est un parallélogramme”, on en déduit que ABA'C est
un parallélogramme. On sait donc que ABA'C est un parallélogramme d’où
d’après la propriété : ”si un quadrilatère est un parallélogramme, alors ses
côtés opposés sont égaux et parallèles” on en déduit que A'B = AC et que
(AC) et (A'B) sont parallèles.
On montre de même en utilisant le parallélogramme ACBC' que
BC' = AC.
A'B = AC et BC' = AC donc A'B = BC' d’où B est le milieu de [A'C'].
On sait que la hauteur (dB) est perpendiculaire au côté (AC) et que (AC)
et (A'B) sont parallèles donc d’après la propriété : ”si deux droites sont
parallèles, toute droite perpendiculaire à l’une est perpendiculaire à
l’autre”, les droites (dB) et (A'C') sont perpendiculaires.
Finalement, (dB) coupe [A'C'] perpendiculairement en son milieu B donc
c’est la médiatrice de [A'C'].
De même, on montre que (dA) est la médiatrice de [B'C'] et que (dC) est la
médiatrice de [A'B'].Les médiatrices d’un triangle sont concourantes donc
les droites (dA), (dB) et (dC) sont concourantes. 
Définition :
Dans un triangle, les médianes sont les droites passant par un sommet et passant par le milieu du côté opposé. |
Propriétés :
|
|
|
Preuve :
Soit ABC un triangle non aplati. On appelle A', B' et C' les milieux
respectifs de [BC], [AC] et [AB]. Soit G le point d’intersection de (CC') et
(BB'). Soit I le point tel que G est le milieu de [AI]. Soit A'' le point
d’intersection de (AG) et de [BC]. Il s’agit donc de montrer que A'' est le
milieu de [BC] c’est à dire que A' et A'' sont confondus. On sait que dans
le triangle ABI, C' est le milieu de [AB] et que G est le milieu de [AI].
D’après la propriété ”si dans un triangle, une droite passe par le milieu de
deux côtés, alors elle est parallèle au troisième” on en déduit que (C'G) est
parallèle à (BI) et d’après la propriété ”si dans un triangle, un segment
joint les milieux de deux côtés, alors sa longueur vaut la moitié de celle du
troisième côté” on en déduit que BI = 2C'G.
De même on montre dans le triangle CAI que les droites (BB') et (CI)
sont parallèles. On sait donc que (BG) est parallèle à (CI) et que (GC) est
parallèle à (BI) donc d’après la propriété ”si un quadrilatère a ses côtés
opposés parallèles, alors c’est un parallélogramme” on en déduit que BGCI
est un parallélogramme. BGCI étant un parallélogramme, d’après la
propriété ”si un quadrilatère est un parallélogramme, alors ses diagonales se
coupent en leur milieu” donc le milieu A' de [BC] est aussi le milieu de la
diagonale [IG] et par conséquent A' et le point d’intersection A'' de (AG)
avec (BC) sont confondus.
Pour montrer que CG =  CC', on sait que BGCI est un parallélogramme
donc d’après la propriété ”si un quadrilatère est un parallélogramme, alors
se côtés opposés ont même longueur” on déduit que GC = BI. Puis, de
GC = BI et de BI = 2C'G on déduit que GC = 2C'G donc
CG = 2C'C + 2CG d’où CG =
CC', on sait que BGCI est un parallélogramme
donc d’après la propriété ”si un quadrilatère est un parallélogramme, alors
se côtés opposés ont même longueur” on déduit que GC = BI. Puis, de
GC = BI et de BI = 2C'G on déduit que GC = 2C'G donc
CG = 2C'C + 2CG d’où CG =  CC'.
CC'.
Définition :
La bissectrice d’un angle est la droite qui partage l’angle en deux angles égaux. |
|
|
Propriétés :
|
Preuve :
Soit ABC un triangle et (dA), (dB) et (dC) les bissectrices des angles  ,
,
 et
et  respectivement.
respectivement.
Soit H le point d’intersection de (dA) et de (dB). D’après la propriété ”Si
un point appartient à la bissectrice d’un angle alors il est à égale distance
des côtés” on en déduit que H est à égale distance de (AB) et de (AC)
d’une part et à égale distance de (AB) et (BC). On en conclut donc que H
est à égale distance de (AC) et (BC). D’après la propriété ”si un point est
à égale distance des côtés d’un angle alors il se trouve sur la bissectrice de
cet angle, on en conclut que H se trouve sur la bissectrice de  c’est à
dire sur (dC). Les trois bissectrices sont donc concourantes en H.
c’est à
dire sur (dC). Les trois bissectrices sont donc concourantes en H.
En outre, si l’on appelle HA le point d’intersection de la perpendiculaire à (BC) passant par H, HB le point d’intersection de la perpendiculaire à (AC) passant par H et HC le point d’intersection de la perpendiculaire à (AC) passant par H, les distances de H à (BC), à (AC) et à (AB) son respetivement données par HHA, HHB et HHC et on a montré qu’elles sont égales donc le cercle de centre H et de rayon HHA passe par les trois points HA, HB et HB.
Propriétés :
|
Preuve :
Propriétés :
|
|
|
||
Preuve :
 et
l’angles
et
l’angles
 sont
symétriques
par
rapport
à
(AI).
La
symétrie
axiale
conserve
les
angles
donc
ces
deux
angles
sont
égaux
et
(AI)
est
aussi
la
bissectrice
de
sont
symétriques
par
rapport
à
(AI).
La
symétrie
axiale
conserve
les
angles
donc
ces
deux
angles
sont
égaux
et
(AI)
est
aussi
la
bissectrice
de
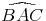 .
.