Vecteurs cours 3e

On dit que deux droites ont la même direction Lorsqu’elles sont parallèles ;
une direction étant donnée par une droite (AB), il existe deux sens de parcours de cette droite.

Soient deux points A et A’ ainsi que la translation qui transforme A en A’. Soient des points B et C ainsi que leurs images par cette translation. On dit que les couples (A ;A’), (B ;B’) et (C ;C’) définissent un vecteur. On note AA' ou BB' ou CC' ou encore . On a donc

AA'= BB'= CC'= u

Remarque :

Dire que AA' = BB' signifie donc :

(AA’) et (BB’) sont parallèles, les deux vecteurs ont donc même direction ;
les deux vecteurs ont le même sens de A vers A’ ;
ils ont la même longueur, AA' = BB'.

Preuve :

Si I est le milieu de [AB] alors AI = IB, A, I et B étant alignés dans cet ordre, les vecteurs et ont même direction et le sens de A vers I est le même que celui de de I vers B ;
Si = alors AI = IB, les droites (AI) et (IB) sont parallèles donc confondues et les points A, I et B sont donc alignés. Ils sont alignés dans cet ordre d’après le sens des vecteurs.

2 Égalité vectorielle et parallélogramme

Soient quatre points A, B, C et D.

Si = alors le quadrilatère ABDC est un parallélogramme ;
Si le quadrilatère ABDC est un parallélogramme, alors = .

Preuve :

On suppose que = , alors les droites (AB) et (CD) sont parallèles et AB = CD. Si un quadrilatère non croisé a deux côtés opposés parallèles et de même longueur, alors c’est un parallélogramme. Donc ABDC est un parallélogramme.
On suppose que ABDC est un parallélogramme. Si un quadrilatère est un parallélogramme, alors ses côtés opposés sont parallèles et de même longueur. Donc AB = CD et (AB) et (CD) sont parallèles. Le sens de A vers B et de C vers D étant les mêmes, on a donc = .

3 Somme de deux vecteurs

Propriété et définition :

Appliquer la translation de vecteur puis la translation de vecteur , revient à appliquer la translation de vecteur . On dit que la composée de deux translations est une translation. On dit aussi que le vecteur est la somme des vecteurs et . On note + = (relation dite de Chasles).

Remarque :

Le vecteur ou est appelé vecteur nul et noté . on a + = .
Le vecteur est appelé le vecteur opposé au vecteur et noté - car + = .

Propriété (règle du parallélogramme) :

Soient trois points A, B et C non alignés. Si M est un point tel que le quadrilatère ABMC est un parallélogramme, alors la somme des vecteurs + est le vecteur .

Preuve :

ABMC est un parallélogramme donc = . Donc + = 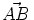+ c’est à dire + = .

4 Composée de deux symétrie centrales

Soient A et B deux points. Appliquer la symétrie centrale de centre A puis la symétrie centrale de centre B revient à appliquer la translation de vecteur = 2 où l’on a noté 2 = + .

Preuve :

Soit M un point, M’ son symétrique par rapport au point A et M” le symétriques de M’ par la symétrie de centre B. M et M’ sont symétriques par rapport à A donc A est le milieu de [MM’]. M” et M’ sont symétriques par rapport à B donc B est le milieu de [M’M”]. Si dans un triangle, un segment joint les milieu de deux côtés du triangle, alors il a pour longueur la moitié du troisième côté. Donc MM'' = 2AB. Soit C le point tel que = 2 ×. Si dans un triangle, une droite passe par les milieux de deux côtés du triangle, alors elle est parallèle au troisième côté. Donc (MM”) et (AB) sont parallèles c’est à dire (MM”) et (AC) sont parallèles. Le sens de M vers M’ étant le même que de A vers C, on en déduit donc que ''
M M = donc ''
M M = 2.