Trigonométrie cours 3e

F.Gaudon

31 décembre 2004

Table des matières

1 Cosinus, sinus et tangente d’un angle aigu
 1.1 Cosinus (rappel)
 1.2 Sinus
 1.3 Tangente
2 Application au calcul d’angles et de longueurs
 2.1 Calcul du sinus, de la tangente ou du cosinus d’un angle dont la mesure est connue
 2.2 Calcul de la mesure d’un angle
  2.2.1 Cas où l’on connaît la mesure de l’angle
  2.2.2 Cas où l’on connaît deux longueurs dans un triangle rectangle
 2.3 Calcul de longueurs
3 Relations trigonométriques
4 Valeurs particulières du cosinus, du sinus et de la tangente
5 Angles inscrits

1 Cosinus, sinus et tangente d’un angle aigu

PICT

1.1 Cosinus (rappel)

Définition :

longueur-du-c^ot´e-adjacent- cos(ABC) = longueur de l’hypot´enuse

1.2 Sinus

Définition :

On appelle sinus de l’angle aigu 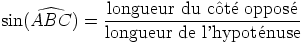ABC, le nombre noté sin ABC défini par :

-longueur--du-c^ot´e-oppos´e- sin(ABC) = longueur de l’hypot´enuse

1.3 Tangente

Définition :

On appelle tangente de l’angle aigu ABC, le nombre noté tan ABC défini par :

tan(ABC) = -longueur--du-c^ot´e-oppose´- longueur du c^ot´e adjacent

Remarque :

Le sinus et le cosinus d’un angle aigu sont compris entre 0 et 1, ce n’est pas le cas de la tangente.

2 Application au calcul d’angles et de longueurs

La calculatrice doit être en mode DEGRÉS.

2.1 Calcul du sinus, de la tangente ou du cosinus d’un angle dont la mesure est connue

Exemple :

Calcul de sin(60o).
On tape 60 sin = ou sin 60 = suivant le modèle de calculatrice.
Il s’affiche 0,86602540.
Attention ce n’est qu’une valeur approchée de sin(60o).
Arrondie à 0,01 près on a : sin(60o) ~~ 0, 87.

2.2 Calcul de la mesure d’un angle

2.2.1 Cas où l’on connaît la mesure de l’angle

Exemple :

Calcul de l’angle x dont la tangente vaut 1, 3.
On tape 1,3 tan-1 = ou tan-1 1,3 = ou 1,3 inv tan = ou1,3 t1an =, etc. suivant les calculatrices.
Il s’affiche 52,43140797.
Attention, ce n’est qu’une valeur approchée.
Arrondie à 0,1 près on a : x ~~ 52, 4o.

2.2.2 Cas où l’on connaît deux longueurs dans un triangle rectangle

Exemple :

Soit EFG un triangle rectangle en F avec EF = 2, 6 cm et EG = 4 cm.
Calcul de l’angle EGF.
Dans le triangle EFG rectangle en F, on connaît le côté opposé à l’angle et l’hypoténuse :

sin EGF = AB-- CB
= 2,6- 4
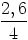= 0, 65
Donc l’angle EGF mesure 40,5o environ.

2.3 Calcul de longueurs

Exemple :

Soit ABD un triangle rectangle en B tel que AB = 9 cm et BAD = 40o.
Calcul de la longueur BD.
Dans le triangle ABD rectangle en B, on connaît l’angle BAD et le côté adjacent, on cherche le côté opposé :

tan BAD = BD ---- BA
tan 40o = BD-- 9
Donc BD = tan 40o× 9 c’est à dire BD ~~ 7, 6 cm.

3 Relations trigonométriques

PICT

Propriété :

Lorsque deux angles sont complémentaires, le sinus de l’un est égal au cosinus de l’autre. C’est à dire, pour tout angle aigu x,

cos(x) = sin(90 - x) et sin(x) = cos(90- x)

Preuve :

cos(ABC) = AB-- BC
= sin(ACB)
= sin(90 -ABC)

Propriété :

Pour tout angle aigu x,

cos2(x) + sin2(x) = 1
où on note
(cos(x))2 = cos2x

Preuve :

cos 2(ABC) + sin 2(ABC) = (AB-- BC)2 + (-AC- BC)2
= AB2 ----2 AC + AC2 ---2- BC
= 2 2 AB---+-AC--- BC2
D’après le théorème de Pythagore dans le triangle ABC rectangle en A : BC2 = AB2 + AC2 Donc
cos 2(ABC) + sin 2(ABC) = BC2 ----2 BC
= 1

Propriété :

Pour tout angle aigu x tel que cos(x)/=0,

tan(x) = sin(x)-- cos(x)

Preuve :

tan(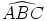ABC) = AC-- AB
sin(ABC) ---------- cos(ABC) = AC- -BACB- BC-
= AC ---- BC ×BC ---- AB
= AC-- AB

4 Valeurs particulières du cosinus, du sinus et de la tangente

anglecosinussinustangente
0o 1 0 0
30o V~ -3- 2 1 2 1 V~ -- 3
45o V~ 22- V~ - 22- 1
60o 1 2 V~ - -3- 2 V~ -- 3

5 Angles inscrits

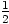Définition :

Sur un cercle C de centre O, on considère trois points A, B et M. L’angle AOB est appelé angle au centre. On dit que l’angle AM B est inscrit dans le cercle si M se trouve du même côté que O par rapport à la droite (AB).

Propriété :

L’angle AM B a pour mesure la moitié de la mesure de l’angle AOB c’est à dire :

AOB = 2 × AM B

Preuve :

admise