Une fraction |
Définition :
Soient a et b deux nombres entiers positifs. On dit que a divise b si il existe un nombre n tel que a × n = b. |
Définition :
Soient a et b deux nombres entiers positifs. |
Un diviseur commun à a et b est un nombre entier qui divise à la fois a et b. |
Exemple :
diviseurs de 8 : 1, 2, 4 et 8 ;
diviseurs de 12 : 1, 2, 3, 4, 6 et 12 ;
diviseurs communs de 8 et 12 : 1, 2 et 4.
Remarque :
Étant donnés deux nombres, le nombre 1 est toujours un diviseur commun de ces deux nombres.
Propriété et définition :
Deux nombres a et b entiers naturels non nuls admettent toujours au moins un diviseur commun. Le plus grand diviseur commun s’appelle le P.G.C.D. (Plus Grand Commun Diviseur) des nombres a et b. On le note PGCD(a; b). |
Preuve :
1 est toujours est un diviseur commun d’où l’existence d’au moins un diviseur commun. Les diviseurs communs de a et b sont inférieurs à a et b, il y en a donc un nombre fini d’où l’existence d’un plus grand diviseur commun.
Exemple :
PGCD(8 ;12)=4
Définition :
Lorsque le plus grand diviseur commun de deux nombres a et b est égal à 1, on dit que les nombres a et b sont premiers entre eux. |
Exemple :
Définition :
Une fraction |
Exemple :
 =
=  =
= 
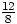 n’est pas irréductible mais
n’est pas irréductible mais  l’est.
l’est.
Propriété :
Pour rendre une fraction |
Preuve :
Soit d le PGCD de a et b. Il existe donc un nombre r tel que dr = a et un nombre s tel que ds = b. On a donc

 est irréductible c’est à dire que r et s sont premiers
entre eux c’est à dire encore que le plus grand diviseur commun à r et s est
1. Soit donc un diviseur n commun à r et s. Il existe donc r' tel que r = r'n
et il existe s' tel que s = s'n. D’où a = dnr' et b = dns' et donc dn est un
diviseur commun à a et b. Comme d est le plus grand, dn = d donc n = 1.
est irréductible c’est à dire que r et s sont premiers
entre eux c’est à dire encore que le plus grand diviseur commun à r et s est
1. Soit donc un diviseur n commun à r et s. Il existe donc r' tel que r = r'n
et il existe s' tel que s = s'n. D’où a = dnr' et b = dns' et donc dn est un
diviseur commun à a et b. Comme d est le plus grand, dn = d donc n = 1.
Propriété :
Si k est un diviseur commun aux deux nombres a et b alors il divise aussi a - b et a + b.
Preuve :
Si k est un diviseur commun de a et b, il existe deux nombres entiers positifs n et p tels que a = kn et b = kp donc a + b = kn + kp c’est à dire a + b = k(n + p) en factorisant par k. Cela montre que k divise aussi a + b. On a de même a-b = k(n-p) ce qui montre que k est un diviseur de a-b.
Propriété :
Soient a et b deux nombres entiers avec a > b et b 0. Si r est le reste de la
division euclidienne de a par b, alors PGCD(a; b) = PGCD(b; r).
0. Si r est le reste de la
division euclidienne de a par b, alors PGCD(a; b) = PGCD(b; r).
Preuve :
r est le reste de la division euclidienne de a par b donc il existe un nombre entier r tel que a = bq + r. On appelle d le PGCD de a et de b. d divise a et b donc il divise bq et a donc il divise aussi a - bq. Mais a - bq = r donc d est un diviseur de r et b. Il reste à montrer que c’est le plus grand diviseur commun à r et b. On considère donc un diviseur commun k à r et b. Il divise donc bq et r donc c’est un diviseur de bq + r et de b c’est à dire de a et de b. Comme d est le plus grand diviseur commun à a et b, k < d donc d est bien le plus grand diviseur commun à b et r.
On suppose que a > b.
Preuve partielle :
Il existe deux entiers naturels q et r tels que a = bq + r avec r < b (division
euclidienne). Si r = 0, a = bq et b = 1b donc b est le PGCD de a et b. Si
r 0, alors il existe q2 et r2 tels que b = q2r + r2 avec r2 < r < b Si r2
0, alors il existe q2 et r2 tels que b = q2r + r2 avec r2 < r < b Si r2 0,
on continue le procédé. Comme les restes r sont des entiers positifs ou nuls
décroissants, l’un des restes r devra être nul et i s’agit de montrer que
l’avant dernier reste non nu et l’on peut montrer que d est le PGCD de a et
b.
0,
on continue le procédé. Comme les restes r sont des entiers positifs ou nuls
décroissants, l’un des restes r devra être nul et i s’agit de montrer que
l’avant dernier reste non nu et l’on peut montrer que d est le PGCD de a et
b.
Exemple :
PGCD de 1078 et 322
| division | a | b | r |
| 1078 = 322 × 3 + 112 | 1078 | 322 | 112 |
| 322 = 112 × 2 + 98 | 322 | 112 | 98 |
| 112 = 98 × 1 + 14 | 112 | 98 | 14 |
| 98 = 14 × 7 | 98 | 14 | 0 |
Technique :
Le PGCD de deux nombres est le même que le PGCD su plus petit et de
la différence des deux.
Par différences successives, on diminue donc les deux nombres, jusqu’à ce
que la différence fasse 0
Exemple :
Calcul du PGCD de 576 et 168 :
| différences | ||
| 576 | 168 | 408 |
| 408 | 168 | 240 |
| 240 | 168 | 72 |
| 168 | 72 | 96 |
| 96 | 72 | 24 |
| 72 | 24 | 48 |
| 48 | 24 | 24 |
| 24 | 24 | 0 |
On a PGCD(576 ;168)=PGCD(408 ;168)=...=PGCD(24 ;24)=24 donc le PGCD est la dernière différence non nulle dans les différences successives.
Preuve :
Soient a et b deux nombres avec a > b, il s’agit de montrer que le PGCD
de a et de b est aussi le PGCD de a - b et de b.
On appelle d le PGCD de a et de b. d divise a et b donc il divise a - b
comme on l’a vu plus haut et il divise b. Donc d est un diviseur de b et de
a - b. Il s’agit donc de montrer que c’est le plus grand. On considère donc
un autre diviseur k de a - b et de b. Il divise donc b et b + (a - b) = a donc
c’est un diviseur de a et de b et il est donc plus petit que d qui est le PGCD
de a et de b. Donc d est bien le plus grand diviseur commun à b et à a - b.
0 ; 1 ; 2 ; etc.
... ; -103 ; ... ; -2 ; -1 ; 0 ; 1 ; 2 ; ...
Définition :
Un nombre décimal est un nombre dont l’écriture à virgule ne comporte qu’un nombre fini de chiffres après la virgule. |
Exemples :
4,25 ; 12 ; 79,066 ; etc.
Définition :
Un nombre rationnel est un nombre qui peut s’écrire sous la forme d’un quotient de deux nombres entiers relatifs. |
Exemples :
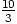
 3, 333 ;
3, 333 ; 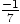 ; 7 =
; 7 = 
Définition :
En nombre irrationnel est un nombre qui n’est pas rationnel. |
Exemple :
 est irrationnel.
est irrationnel.
Preuve :
Supposons que  est rationnel.
est rationnel.
On donc peut trouver deux nombres entiers relatifs a et b tels que  =
=  .
On peut même supposer que la fraction
.
On peut même supposer que la fraction  est irréductible, c’est à dire que a
et b sont premiers entre eux. Alors :
est irréductible, c’est à dire que a
et b sont premiers entre eux. Alors :




 est don irrationnel.
est don irrationnel.