a désigne un nombre fixé. Le procédé f qui à tout nombre x associe le nombre ax est appelé fonction linéaire. On note  |
Définition :
a désigne un nombre fixé. Le procédé f qui à tout nombre x associe le nombre ax est appelé fonction linéaire. On note  |
Exemple :
la fonction linéaire f de coefficient 4 associe au nombre 3 le nombre 3 × 4 c’est à dire 12. On écrit f(3) = 12. Elle associe au nombre -3, 1 le nombre -12, 4, c’est à dire f(-3, 1) = -12, 4.
Définition :
Soient a et b deux nombres. On définit une fonction affine f lorsqu’à chaque nombre x on associe le nombre ax + b. On note f : x Le nombre ax + b est appelé l’image du nombre x par la fonction f |
Exemple :
f : x - 2x + 5
- 2x + 5
f(0) = -2 × 0 + 5
f(0) = 5
5 est l’image de 0 par la fonction affine f.
f( ) = -2 ×
) = -2 × + 5
+ 5
f( ) = -3 + 5
) = -3 + 5
f( ) = 2
) = 2
2 est l’image de  par la fonction affine f.
par la fonction affine f.
Remarque :
f est de la forme f : x ax lorsque b = 0.
ax lorsque b = 0.
Toute fonction linéaire est donc une fonction affine.
Définition :
La représentation graphique d’une fonction f dans un repère donné est l’ensemble des points de coordonnées (x; f(x)). |
Propriété :
La représentation graphique de la fonction affine f : x |
Les points de cette droite sont les points dont les coordonnées (x; y) vérifient l’équation y = ax + b. |
On dit que cette droite a pour équation y = ax + b. |
Définition :
On considère la fonction affine f : x
|
Exemple :
f : x 0, 5x + 3
0, 5x + 3
Soit (D1) sa représentation graphique.
f(0) = 3 donc A(0; 3) appartient à (D1).
f(-2) = 2 donc B(-2; 2) appartient à (D1).
On obtient le tableau de valeurs suivant :
| x | 0 | 1 |
| f(x) | 4 | 7 |
Propriété et définition :
Dans un repère, la représentation graphique de la fonction linéaire de coefficient a est la droite qui passe par l’origine O du repère et par le point de coordonnées (1; a). On dit que cette droite a pour équation y = ax et que a est son coefficient directeur. |
preuve :
la représentation graphique est formée des points de coordonnées (x; ax). On admettra qu’ils sont alignés. Les points de coordonnées (0; a × 0) et (1; a × 1) c’est à dire (0; 0) et (1; a) sont donc sur cette droite.
Exemple :
On considère un carré de côté x cm.
| x | 3 | 3,5 | 5 |
| p(x) | 12 | 14 | 20 |
Ce tableau est un tableau de proportionnalité de coefficient 4. Le procédé p qui, à un nombre x associe le nombre 4x est une fonction linéaire de coefficient 4. On a p(3) = 4, p(3, 5) = 14, etc.
| x | 3 | 3,5 | 4 |
| A(x) | 9 | 12,25 | 16 |
Ce tableau n’est pas un tableau de proportionnalité. A n’est pas une fonction linéaire.
Propriété :
Deux grandeurs sont proportionnelles lorsque l’une est une fonction linéaire de l’autre. Le coefficient de la fonction linéaire est alors aussi un coefficient de proportionnalité. |
Preuve :
Deux grandeurs x et y sont proportionnelles si les valeurs de y s’obtiennent en multipliant les valeurs de x correspondantes par un même nombre a c’est à dire si y est une fonction linéaire de coefficient a des valeurs de x.
Propriété :
|
preuve :
 et
par
suite
le
nombre
x
devient
après
augmentation
x +
et
par
suite
le
nombre
x
devient
après
augmentation
x +  x = (1 +
x = (1 +  )x = 1, 15x ;
)x = 1, 15x ;
 et
par
suite
le
nombre
x
devient
x -
et
par
suite
le
nombre
x
devient
x - x = (1 -
x = (1 -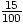 )x = 0, 85x.
)x = 0, 85x.
Propriété :
Pour une fonction affine f définie par f(x) = ax+b, il y a proportionnalité entre les accroissements de x et les accroissements de f(x). Plus précisément, lorsque x augmente de k, f(x) augmente de ka. |
Preuve :
Soit f la fonction définie par f(x) = ax + b.
Pour tous les nombres x et y, l’accroissement des valeurs de f vaut f(x) -f(y), il
sagit de justifier qu’il est proportionnel à l’accroissement x - y de x à y, c’est à
dire que les quotients  sont tous égaux indépendamment de x et y.
Or,
sont tous égaux indépendamment de x et y.
Or,
 | =  | ||
=  | |||
=  | |||
= 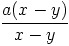 | |||
| = a | |||
Exemple :
Soit f la fonction linéaire telle que f(3) = 12, 6.
f est linéaire donc de la forme f : x ax avec a à déterminer.
ax avec a à déterminer.
Or f(3) = 12, 6 et f(3) = a × 3 donc a × 3 = 12, 6.
D’où a =  c’est à dire a = 4, 2.
c’est à dire a = 4, 2.
Donc f : x 4, 2x.
4, 2x.
Propriété :
Le coefficient directeur a d’une fonction affine f telle que f(xA) = yA et f(xB) = yB est donné par : 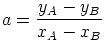 |
Preuve :
Voir paragraphe précédent.
Exemple :
Déterminer la fonction affine f telle que f(3) = 9 et f(-2) = -1. f est une
fonction affine donc de la forme f : x ax + b avec a et b deux nombres à
déterminer.
ax + b avec a et b deux nombres à
déterminer.
On a vu que les accroissements sont proportionnels avec pour coefficient de
proportionnalité a.
Donc a =  =
=  =
=  = 2.
= 2.
En outre f(3) = 9 et f(3) = 3a + b c’est à dire f(3) = 3 × 2 + b donc
3 × 2 + b = 9 c’est à dire 6 + b = 9 ou encore b = 3.
f est la fonction définie par f(x) = 2x + 3.