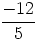Exemple :
-
L’équation
suivante
est
du
premier
degré
car
le
nombre
x
est
élevé
à
la
puissance
1.
La
seule
inconnue
est
le
nombre
x.
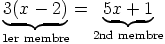
-
L’équation
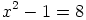
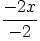
 (on divise par 6 les deux membres de l’égalité)
(on divise par 6 les deux membres de l’égalité)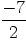
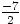 .
. ou
ou 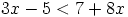

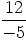 on divise par -5, l’ordre est inversé
on divise par -5, l’ordre est inversé