La fonction carré est la fonction f définie sur  |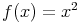
Définition :
La fonction carré est la fonction f définie sur |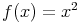
Variations :
La fonction carré est :
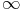; 0] ;
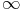[.Elle admet un minimum égal à 0 en 0.
| x | -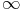 | 0 | + |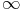
||
| f(x) |  | 0 |  | ||
Preuve :
Soient x et y deux nombres réels tels que 0 < x < y. On a donc y - x > 0.
Alors f(y) - f(x) = y2 - x2 = (y - x)(y + x). Or x + y > 0 et y - x > 0 on
a donc f(y) - f(x) > 0 c’est à dire f(y) > f(x) ce qui montre que f est
croissante sur [0; +[.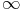
Soient x et y deux nombres réels tels que x < y < 0. On a donc y - x > 0 à nouveau.
Alors f(y) - f(x) = y2 - x2 = (y - x)(y + x). Comme x et y sont négatifs,
x + y < 0. De y - x > 0 on déduit donc que f(y) - f(x) < 0 c’est à dire
f(y) < f(x) ce qui montre que f est décroissante sur ] -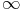; 0].
En outre, comme le carré d’un nombre réel est toujours positif, on a donc pour tout nombre réel x, f(x) > 0 et f(0) = 0 d’où le minimum de f en 0.
Représentation graphique :
La représentation graphique de la fonction carré est appelée parabole.
Ci-dessous, on peut visualiser le tracé des points de la parabole : pour tout réel a (faire varier le curseur), le point M a pour abscisse a et pour ordonnée a².
Définition :
On appelle fonction inverse la fonction f définie pour tout nombre réel différent de 0 par  |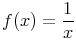
Variations :
La fonction inverse est :
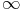; 0[ ;
[.
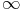| f(x) | -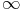 | 0 | + |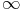
||
| x |  |  |  | ||
Preuve :
Soient x et y deux nombres réels différents de 0 du même intervalle
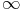] -; 0[ ou ]0; +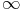[ et tels que x < y.
On a
| f(y) - f(x) | =  - | ||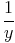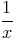
=  - | |||
=  |
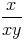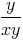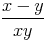Or x < y donne x - y < 0, x et y sont de même signe donc xy > 0 d’où f(y) - f(x) < 0 c’est à dire f(y) < f(x) donc f est décroissante sur cet intervalle.
Représentation graphique :
La représentation graphique de la fonction inverse est appelée hyperbole.
Ci-dessous, on peut visualiser le tracé des points de l'hyperbole : pour tout réel non nul a (faire varier le curseur), le point M a pour abscisse a et pour ordonnée l'inverse de a.
Définition :
Soient m et p deux nombres réels. On appelle fonction affine la fonction
f définie sur  |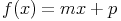
Variations :
;
;
.
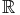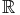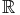| x | - | + |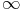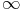
|
| f(x) |  | ||
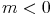
| x | - | + |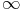
|
| f(x) |  | ||
Preuve :
Soient x et y deux nombres réels tels que x < y.
On a f(y) - f(x) = my + p - (mx + p) = my - mx + p - p = m(y - x).
Or x < y implique y - x > 0.
Représentation graphique :
La représentation graphique de toute fonction affine est une droite.