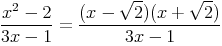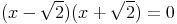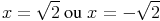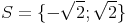Méthode :
Soient a et b deux nombres réels avec a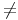 0.
0.
Étudier le signe du nombre ax + b signifie déterminer les valeurs de x pour lesquelles ax + b > 0 et celles pour lesquelles ax + b < 0.
Méthode :
Soient a et b deux nombres réels avec a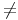 0.
0.
Étudier le signe du nombre ax + b signifie déterminer les valeurs de x pour lesquelles ax + b > 0 et celles pour lesquelles ax + b < 0.
Synthèse :
On résume l’étude dans un tableau de signe :
Si a > 0
| x | - | -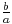 | + |
||
| signe | |||||
| de | - | 0 | + | ||
| ax + b | |||||
Si a < 0
| x | - | -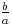 | + |
||
| signe | |||||
| de | + | 0 | - | ||
| ax + b | |||||
Propriété :
ax + b est du signe de a pour les valeurs de x supérieures à - |
Exemple d’étude de signe d’un produit :
On considère le produit
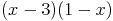
On fait apparaître dans un tableau de signes, les signes de x - 3 et de 1 - x, puis on utilise la règle des signes.
| x | - | 1 | 3 | + |
|||
| x - 3 | - | - | 0 | + | |||
| 1 - x | + | 0 | - | - | |||
| (x - 3)(1 - x) | - | + | - | ||||
Exemple d’étude de signe d’un quotient :
On considère le quotient
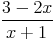
 0
c’est
à
dire
x
0
c’est
à
dire
x - 1.
- 1.
| x | - | -1 | 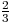 | + |
|||
| 3 - 2x | + | + | 0 | - | |||
| x + 1 | - | 0 | + | + | |||
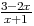 | - | || | + | 0 | - | ||
Définition :
|
Définition :
Soient I et J deux intervalles.
|
On considère l’inéquation
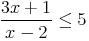
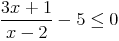
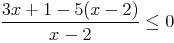
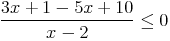
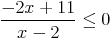
| x | - | -5,5 | 2 | + |
|||
| -2x + 11 | + | 0 | - | - | |||
| x - 2 | - | - | 0 | + | |||
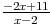 | - | 0 | + | || | - | ||
![S = [- oo ; - 5,5] U ]2;+o o [](equationssignescourshtml17x.gif)
On considère l’équation

 .
.