| Soit D une droite dans le plan muni d’un repère (O; On appelle équation de la droite (D) toute équation vérifiée par et uniquement par les coordonnées (x; y) des points de la droite (D). |
Définition :
| Soit D une droite dans le plan muni d’un repère (O; On appelle équation de la droite (D) toute équation vérifiée par et uniquement par les coordonnées (x; y) des points de la droite (D). |
Exemple :
La droite (D) ci-dessous a pour équation y = 3x + 2 mais aussi y - 3x - 2 = 0.
Un point M(x; y) appartient à la droite (D) si et seulement si x et y vérifient y = 3x + 2.
Théorème et définition :
| Soit (O;
|
Preuve :
Soit (D) la droite passant par les points A(xA; yA) et B(xB; yB) distincts.
Soit M(x; y) un point quelconque.
Les vecteurs 
et 
ont pour coordonnées respectives (x - xA; y - yA)
et (xB - xA; yB - yA).
M appartient à (D) signifie que les vecteurs 
et 
sont colinéaires ce
qui se traduit par :
xA
d’où
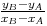et
p = yA - xA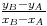
.
Exemple :
Soit D la droite passant par les points A et B de coordonnées (1; 3) et (-2; 5).
xA
xB donc D n’est pas parallèle à l’axe des ordonnées. Son équation est
donc de la forme y = mx + p.
m = 
= 
= 
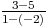donc son équation est y = 
x + b.
Or A 
D donc ses coordonnées vérifient l’équation d’où 3 = 
× 1 + b. et
b = 3 + 
c’est à dire b = 
.
L’équation est donc y =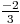 
x + 
.
Remarque :
Toute équation de la forme ax + by + c = 0 avec (a; b)
(0; 0) est l’équation
d’une droite.
Définition :
| On appelle vecteur directeur d’une droite D tout vecteur non nul de direction parallèle à cette droite. |
Propriété :
| Dans le plan muni d’un repère (O; |
Preuve :
On considère les points A(0; p) et B(1; m + p).
Ces deux points appartiennent à la droite D puisque leur coordonnées vérifient l’équation y = mx + p.
Le vecteur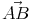 
est un vecteur directeur et a pour coordonnées
(xB - xA; yB - yA) soit (1 - 0; m + p - p) donc (1; m).
Exemple :
Soit D la droite passant par A(1; 3) et de vecteur directeur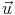 
(2; 4).
M D si et seulement si 
est colinéaire à 
c’est à dire 
de coordonnées (x - 1; y - 3) est colinéaire à 
de
coordonnées (2; 4)
c’est à dire si et seulement si 2(x - 1) - 4(y - 3) = 0 (condition de colinéarité de deux vecteurs)
c’est à dire si et seulement si 2x - 2 - 4y + 12 = 0 ou encore 4y = 2x + 10
et y = 
x +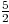 
.
D’où l’équation de la droite.
Propriété :
| Deux droites (D) et (D') d’équations réduites respectives y = mx + p et y = m'x + p' sont parallèles si et seulement si m = m'. |
Preuve :
Soient 
de coordonnées (1; m) et 
de coordonnées (1; m') des vecteurs
directeurs de (D) et (D') respectivement.
Les deux droites sont parallèles si et seulement si leurs vecteurs directeurs ont même direction c’est à dire sont colinéaires c’est à dire si et seulement si 1 × m = 1 × m'.
Définition :
| Résoudre le système d’équations :  |
Théorème :
| On considère le système (S) suivant :   (0; 0) et
(a'; b') (0; 0).
Les solutions du systèmes sont les couples de coordonnées des points
communs aux deux droites (D) et (D') d’équations ax + by = c et
a'x + b'y = c' respectivement dans un repère (O;
|
Propriété :
| Le système (S) suivant :   0.
Si a'b-ab' = 0, alors le système admet ou bien une infinité de solutions, ou bien aucune solution. |
Preuve :
Dans le cas où b et b' sont non nuls, le système est équivalent à
y = 
x + c et y = 
+ c'.
Le système admet une unique solution si et seulement si les droites
correspondantes sont sécantes c’est à dire si et seulement si les coefficients
directeurs sont égaux sont égaux c’est à dire encore 
= 
qui s’écrit
encore a'b - ab' = 0.
Exemple :
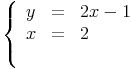
Exemple :
; -
).
; 
).
; 
) un repère.
où 
; 
), le vecteur 
de coordonnées (1; 
; 
).