Généralités fonctions, cours, classe de 2nde
Cliquer sur la loupe pour tout révéler ou masquer :
Cliquer sur les ____ pour révéler ou masquer élément par élément.
I - Notions Fondamentales sur les fonctions
Définition :
- Une fonction est un procédé qui ____ permet d'associer à tout nombre x, élément d'un ensemble E de départ, un nombre unique noté f(x).
- L'ensemble E est ____l'ensemble de définition de la fonction f.
- Le nombre f(x) est appelé ____l'image du nombre x par la fonction f.
- Le nombre x est appelé ____antécédent du nombre f(x).
Exemples :[Calcul d'images et d'antécédents par une fonction]
- Soit g la fonction définie pour tout réel x par $g(x)=x^2-4x+32$.
Calcul de $g(-5)$ :
____$g(-5)=(-5)^2-4\times(-5)+32=25+20+32=77$.
-5 a donc pour image ____77 par la fonction g ce qui signifie aussi que -5 est un ____antécédent de ____77 par la fonction g.
- Recherche du ou des antécédents de 6 par la fonction $h$ définie pour tout réel $x$ par $h(x)=3x+5$.
Un réel $x$ est un antécédent de 6 par $h$ si et seulement si ____$h(x)=6$ c'est à dire $3x+5=6$
donc $3x=1$ c'est à dire $x=\frac{1}{3}$.
$\frac{1}{3}$ est donc l'unique antécédent de 6 par la fonction $h$.
Définition :
Pour présenter des nombres et leurs images par une fonction, on utilise un ____tableau de valeurs.
Exemple : [Construire un tableau de valeurs]
Pour la fonction g définie par $g(x)=x^2-4x+32$ :
_____
II - Intervalles de nombres réels
Définition :
On appelle ensemble des ____nombres réels, noté ____$\mathbb{R}$, l'ensemble des abscisses des points de toute droite graduée (par exemple 1, -3, $\sqrt{2}$, $\pi$, etc).
Définitions :
Soient a et b deux nombres réels avec a inférieur à b.
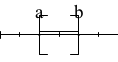
- [a ; b] est l'ensemble des réels x tels que ____$a\leq x\leq b$. On l'appelle ____intervalle fermé d'extrémités a et b.
- ]a ; b[ est l'ensemble des réels x tels que ____$a< x< b$. On l'appelle ____ intervalle ouvert d'extrémités a et b.
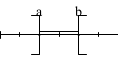
- [a ; b[ est l'ensemble des réels x tels que _____ $a\leq x< b$. Cet intervalle est dit ____ ouvert en b et fermé en a.
- $[a ; +\infty[$ est l'ensemble des réels x tels que _____ $a\leq x$.
- $]-\infty; b[$ est l'ensemble des réels x tels que _____ $x < b$.
III - Transformations d'écritures
Propriété :
- Pour tous les nombres réels a, b et k :
____$$k(a+b)=ka+kb$$
- Pour tous les nombres réels a, b, c et d :
____$$(a+b)(c+d)=ac+ad+bc+bd$$
Propriété : identités remarquables
Pour tous les réels a et b :
____
$$(a+b)^2=a^2+2ab+b^2$$
____
$$(a-b)^2=a^2-2ab+b^2$$
____
$$(a-b)(a+b)=a^2-b^2$$
Exemple : [Savoir développer une expression littérale]
- Pour tout réel x, $A(x)=(2x+4)(x-5)$____$=2x\times x+4x - 2x\times5 - 20$ par la double distributivité
D'où $A(x)=2x^2+4x-10x-20=2x^2-6x-20$
- Pour tout réel x, $B(x)=(x-2)^2+28$____$=x^2-2\times 2\times x+2^2+28$ d'après l'identité remarquable $(a+b)^2=a^2+2ab+b^2$
D'où $B(x) =x^2-4x+32=g(x)$.
IV - Représentation graphique
Défintion : courbe représentative
- Soit f une fonction définie sur un ensemble E de $\mathbb{R}$.
On appelle courbe représentative de f l'ensemble des points M du plan de coordonnées _____(x ; f(x)) dans un repère du plan avec x parcourant l'ensemble de définition E.
- Un point M de coordonnées (x ; y) appartient donc à la courbe si et seulement si ses coordonnées vérifient ____ l'équation y = f(x) appelée ____ équation de la courbe représentative $\mathcal{C}_f$ de la fonction f.
Exemple :
Ci-dessous, la représentation graphique $\mathcal{C}$ de la fonction g définie par $g(x)=x^2-4x+32$ sur l'intervalle [0 ; 8].
Propriété : lectures graphiques
Soit $\mathcal{C}$ la courbe représentative d'une fonction f.
- L'image f(x) d'un nombre x par f se lit sur l'axe des _____ ordonnées : c'est ______ l'ordonnée du point d'intersection de la courbe $\mathcal{C}$ avec la droite parallèle à l'axe des ordonnées passant par le point de coordonnées $(x;0)$.
- Les antécédents, s'il en existe, de tout nombre y par f se lisent sur l'axe des _____ abscisses : ce sont les ______ abscisses des points d'intersection de la courbe $\mathcal{C}$ avec la droite parallèle à l'axe des abscisses et passant par le point de coordonnées $(0;y)$.
Exemple :[Lire graphiquement des images et des antécédents]
Sur la courbe ci-dessus représentant la fonction g :
- L'image de 1 est ____29;
- 32 a deux antécédents qui sont ____0 et 4 ;
V - Résolutions graphiques d'équations
Définition :
Soit k un nombre réel, f une fonction et $\mathcal{C}_f$ sa représentation graphique dans un repère.
Les solutions de l'équation f(x) = k sont ____ les abscisses des points d'intersection de la courbe avec la droite parallèle à l'axe des abscisses et passant par le point de coordonnées (0 ; k).
Exemple : [Lire graphiquement les solutions d'une équation]
Ci-dessus, les solutions de l'équation f(x) = -0,5 sont environ ____ -2,5 ; 2,5 et 3 par lecture graphique.
Propriété : résolution graphique d'équation avec deux fonctions
Soient f et g deux fonctions et $\mathcal{C}_f$ et $\mathcal{C}_g$ leur représentation graphique dans un repère.
Les solutions de l'équation $f(x)=g(x)$ sont les ____abscisses des points d'intersection de la courbe $\mathcal{C}_f$ et de $\mathcal{C}_g$.
Exemple :
Ci-dessus, $\mathcal{C}_f$ est la courbe bleue et $\mathcal{C}_g$ est la courbe verte.
L'ensemble des solutions de l'équation $f(x)=g(x)$ semble être par lecture graphique ____{-3;1}.