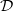 ) et
) et 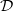 ′ deux droites distinctes. Les configurations suivantes sont les seules possibles :
′ deux droites distinctes. Les configurations suivantes sont les seules possibles :
Définition :
| Deux droites de l’espace sont dites :
|
Propriété :
Soient (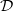 ) et
) et 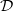 ′ deux droites distinctes. Les configurations suivantes sont les seules possibles :
′ deux droites distinctes. Les configurations suivantes sont les seules possibles :
| Droites non coplanaires | Droites coplanaires sécantes | Droites parallèles |
Remarque :
Deux droites non coplanaires n’ont donc aucun point commun et ne sont pourtant pas non plus parallèles. Ceci n'est possible que dans l'espace.
Définition :
| Deux plans sont parallèles si ils n’ont aucun point commun. |
Propriété :
| Deux plans sécants se coupent selon une droite. |
Propriété :
Soient ( ) et (
) et ( ′) deux plans distincts. Les configurations suivantes sont les seules possibles :
′) deux plans distincts. Les configurations suivantes sont les seules possibles :
| Plans parallèles | Plans sécants |
Définition :
| Une droite est parallèle à un plan si elle n’a aucun point commun avec ce plan. |
Remarque :
On a vu précédemment que deux droites qui n’ont aucun point commun ne sont pas nécessairement parallèles.
Propriété :
| Une droite ( |
Synthèse :
| Droite sécante au plan : | Droite parallèle au plan : | Droite incluse dans le plan : |
| intersection réduite à un point | pas de point d’intersection | une infinité de points d’intersection |
Propriété :
| Deux plans sont parallèles si l’un contient deux droites sécantes parallèles à l’autre. |
Propriété :
| Si deux plans sont parallèles, alors tout plan qui coupe l’un coupe l’autre et les droites d’intersection sont parallèles. |