Repérage dans le plan, cours pour la classe de seconde

F.Gaudon

15 mai 2010

Table des matières

1 Coordonnées dans un repère du plan
2 Milieu d’un segment et distance dans un repère orthonormé
2.1 Milieu d’un segment
2.2 Distance entre deux points

1 Coordonnées dans un repère du plan

Définition :

On appelle ensemble des nombres entiers naturels et on note ℕ, l’ensemble des nombres 0, 1, 2, ..., 10, 11,... 123,... .
On appelle ensemble des nombres entiers relatifs et on note ℤ, l’ensemble des nombres ...,-87, .., -3,-2,-1,0,1,2, ...,15,... .
On appelle ensemble des nombres réels et on l’ensemble des abscisses des points d’une droite graduée.

Propriété et définition :

Un repère orthonormal du plan est défini par la donnée de trois points non alignés O, I et J formant un triangle rectangle isocèle de sommet O. On note alors (O; I; J) le repère ainsi défini.

Á tout point M du plan, on associe un unique couple (x; y) de nombres réels appelé couple de coordonnées du point M dans le repère (O; I; J). x est appelé abscisse du point M et y est appelé ordonnée du point M.

Déplacer le point M.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

F.Gaudon, Créé avec GeoGebra

2 Milieu d’un segment et distance dans un repère orthonormé

2.1 Milieu d’un segment

Propriété :

Soient A et B deux points de coordonnées respectives (x_A; y_A) et (x_B; y_B) d’un repère (O; I; J). Alors le milieu I du segment [AB] a pour abscisse la moyenne des deux abscisses et pour ordonnée la moyenne des ordonnées, c’est à dire, a pour coordonnées :

xA + xB xI = -------- 2

y + y yI = -A----B- 2

Preuve :

Cas où x_A = x_B ou y_A = y_B : on supposera y_A = y_B et y_A > y_B (la démonstration se ferait de la même manière pour x_A = x_B). I est le milieu de [AB] si et seulement si IA = IB et I appartient à [AB], c’est à dire y_I = y_A = y_B et x_I - x_A = x_B - x_I donc 2x_I = x_B + x_A et x_I = .
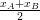Cas où x_A≠x_B et y_A≠yB. Soit C le point tel que x_C = x_B et y_C = y_A. On note K le milieu de [AC]. D’après le théorème des milieux, (IK) est parallèle à (BC) donc x_I = x_K et d’après le cas précédent x_K = d’où le résultat. On utilise de même le milieu J de [BC] pour montrer que y_I = .

Déplacer les points A et B.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

F.Gaudon, Créé avec GeoGebra

Exemple :

Soient A(2; -1) et I(4; 2). Le point B(x; y) tel que I est le milieu de [AB] vérifie 4 = 2+2x) et 2 = --1+2y- donc 2 + x = 8 et -1 + y = 4 d’où x = 6 et y = 4 + 1 c’es à dire y = 5.

Algorithmique :

Algorithme de calcul des coordonnées du milieu du segment [AB] avec A et B de coordonnées respectives (x_A; y_A) et (x_B; y_B) :

Entrées : x_A, y_A, x_B, y_B
Début traitement
x_I prend la valeur ;
y_I prend la valeur .
Fin traitement.
Sorties : x_I, y_I

2.2 Distance entre deux points

Propriété :

On considère deux points A et B de coordonnées (_A; y_A) et (x_B; y_B) dans un repère (O; I; J) orthonormal. Alors la distance AB est donnée par :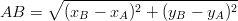

∘ ------------------------ AB = (xB - xA )2 + (yB - yA )2

ce qui s’écrit aussi :

AB = ∘y------y-)2 +-(x----x-)2 B A B A

Preuve :

On supposera afin d’alléger les écritures que x_A < x_B et y_A < y_B, les autres cas se démontrant de la même manière. Soit H le point de coordonnées (x_B; y_A). Le repère est orthonormal donc les droites (AH) et (BH) sont perpendiculaires en H et l’unité est la même sur les deux axes. La distance AH vaut x_B - x_A et la distance BH est y_B - y_A. Dans le triangle ABH rectangle en H, le théorème de PYTHAGORE permet donc d’écrire que AB² = AH² + BH² c’est à dire AB² = (x_B - x_A)² + (y_B - y_A)² d’où la formule.

Déplacer A ou B.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

F.Gaudon, Créé avec GeoGebra

Algorithmique :

Algorithme de calcul de la distance entre deux points A et B de coordonnées respectives (x_A; y_A) et (x_B; y_B) :

Entrées : x_A, y_A, x_B, y_B

Début traitement :

d prend la valeur ∘ ----------2------------2
(xB - xA) + (yB - yA)

Fin traitement.

Sorties : d

Entrer xA
Entrer yA
Entrer xB
Entrer yB

Entrer xA
Entrer yA
Entrer xB
Entrer yB